Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi đths y = ax + b là (d)
Vì \(\left(\sqrt{2};4-\sqrt{2}\right)\in\left(d\right)\Rightarrow4-\sqrt{2}=a\sqrt{2}+b\)
vì \(\left(2;\sqrt{2}\right)\in\left(d\right)\Rightarrow\sqrt{2}=2a+b\)
Ta có hệ \(\hept{\begin{cases}a\sqrt{2}+b=4-\sqrt{2}\\2a+b=\sqrt{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a\sqrt{2}-2a=4-\sqrt{2}-\sqrt{2}\\2a+b=\sqrt{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a\left(\sqrt{2}-2\right)=4-2\sqrt{2}\\2a+b=\sqrt{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=-2\\2.\left(-2\right)+b=\sqrt{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=-2\\b=4+\sqrt{2}\end{cases}}\)

a) Do parabol qua điểm O nên ta có thể giả sử phương trình của Parabol có dạng : y = ax2 \(\left(a\ne0\right)\)
Parabol qua điểm \(M\left(\sqrt{3};3\right)\) nên ta thấy ngay \(3=a\left(\sqrt{3}\right)^3\Rightarrow a=1\)
Vậy phương trình parabol là \(y=x^2\)
Ta có bảng giá trị:
| x | 2 | 1 | 0 | -1 | -2 |
| y | 4 | 1 | 0 | 1 | 4 |
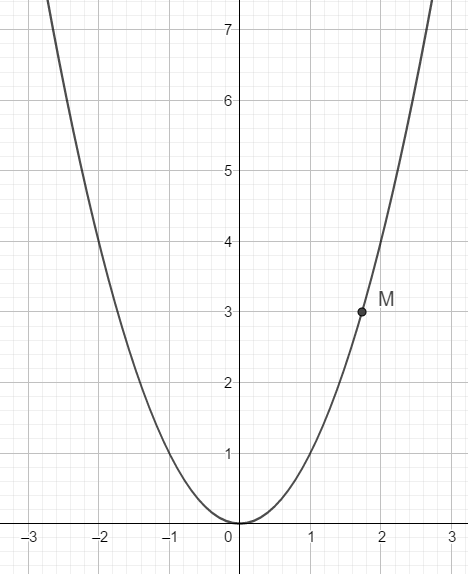
b) Vì \(K\left(\sqrt{2};4\right)\) thuộc parabol (P) nên \(4=a\left(\sqrt{2}\right)^2\Leftrightarrow a=2\)
Vậy phương trình parabol cần tìm là: \(y=2x^2\)
Bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 8 | 2 | 0 | 2 | 8 |
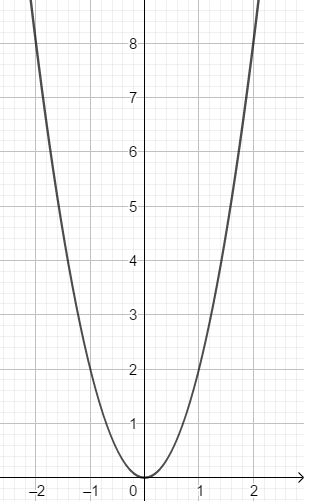

Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot\sqrt{2}+b=4-\sqrt{2}\\2a+b=\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\left(\sqrt{2}-2\right)=4-2\sqrt{2}\\2a+b=\sqrt{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{4-2\sqrt{2}}{\sqrt{2}-2}=-2\\b=\sqrt{2}+4\end{matrix}\right.\)

Vì đồ thị hàm số y=ax+b đi qua điểm(\(\sqrt{2}\) ; 4) và (2;\(\sqrt{2}\)) nên ta có hệ phương trình:\(\left\{{}\begin{matrix}4=\sqrt{2}a+b\\\sqrt{2}=2a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4\sqrt{2}=2a+\sqrt{2}b\\\sqrt{2}=2a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{2}=\left(\sqrt{2}-1\right)b\\\sqrt{2}=2a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{3\sqrt{2}}{\sqrt{2}-1}\\\sqrt{2}=2a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=6+3\sqrt{2}\\\sqrt{2}=2a+6+3\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=6+3\sqrt{2}\\a=-3-\sqrt{2}\end{matrix}\right.\)Vậy a=-3-\(\sqrt{2}\) và b=6+3\(\sqrt{2}\)

Đồ thị hàn số y = a\(x\) + b đi qua các điểm A (\(\sqrt{2}\); 4 - \(\sqrt{2}\)) vàB (2; \(\sqrt{2}\))
Thay tọa độ điểm A, B vào pt đồ thị ta có:
\(\left\{{}\begin{matrix}\sqrt{2}.a+b=4-\sqrt{2}\\2a+b=2+\sqrt{2}\end{matrix}\right.\)
Trừ vế cho vế ta có: 2a + b - (\(\sqrt{2}\)a + b) = 2 + \(\sqrt{2}\) - (4 - \(\sqrt{2}\))
2a + b - \(\sqrt{2}\)a - b = -2 + 2\(\sqrt{2}\)
2a - \(\sqrt{2}\)a = - 2 + 2\(\sqrt{2}\)
a.(2 - \(\sqrt{2}\)) = -2 + 2\(\sqrt{2}\)
a = (-2 + 2\(\sqrt{2}\)) : (2 - \(\sqrt{2}\))
a = \(\sqrt{2}\)
b = 2 + \(\sqrt{2}\) - 2\(\sqrt{2}\)
b = 2 - \(\sqrt{2}\)

Thay \(x=\sqrt{2},y=4-\sqrt{2}\) vào đồ thị ta có pt: \(\sqrt{2}a+b=4-\sqrt{2}\)
Thay \(x=2,y=\sqrt{2}\) vào đồ thị ta có pt: \(2a+b=\sqrt{2}\)
Ta có hpt: \(\left\{{}\begin{matrix}\sqrt{2}a+b=4-\sqrt{2}\\2a+b=\sqrt{2}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=4+\sqrt{2}\end{matrix}\right.\)
Theo đề bài ta có:\(\left\{ \begin{array}{l} 4 - \sqrt 2 = \sqrt 2 a + b\\ \sqrt 2 = 2a + b \end{array} \right.\) \(\Rightarrow HPT\) vô nghiệm
Không tìm được $a,b$ thỏa mãn