Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hàm số đã cho là y = 2x + b.
Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3.
Vậy hàm số đã cho là y = 2x - 3.
b) Hàm số đã cho là y = 3x + b.
Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4.
Vậy hàm số đã cho là y = 3x - 4.
c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b.
Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5.
Vậy hàm số đã cho là y = √3x + 5.
Bài giải:
a) Hàm số đã cho là y = 2x + b.
Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3.
Vậy hàm số đã cho là y = 2x - 3.
b) Hàm số đã cho là y = 3x + b.
Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4.
Vậy hàm số đã cho là y = 3x - 4.
c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b.
Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5.
Vậy hàm số đã cho là y = √3x + 5

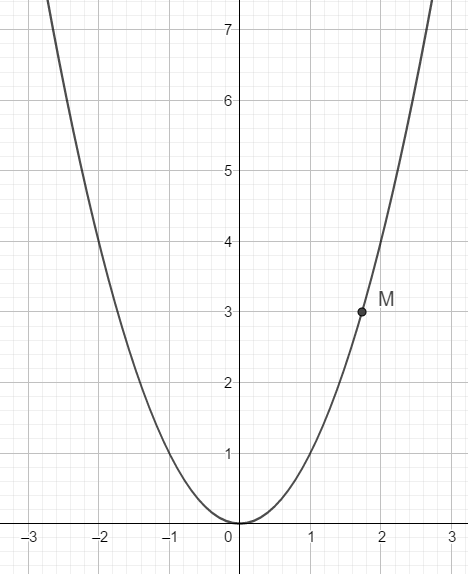
a) Do parabol qua điểm O nên ta có thể giả sử phương trình của Parabol có dạng : y = ax2 \(\left(a\ne0\right)\)
Parabol qua điểm \(M\left(\sqrt{3};3\right)\) nên ta thấy ngay \(3=a\left(\sqrt{3}\right)^3\Rightarrow a=1\)
Vậy phương trình parabol là \(y=x^2\)
Ta có bảng giá trị:
| x | 2 | 1 | 0 | -1 | -2 |
| y | 4 | 1 | 0 | 1 | 4 |
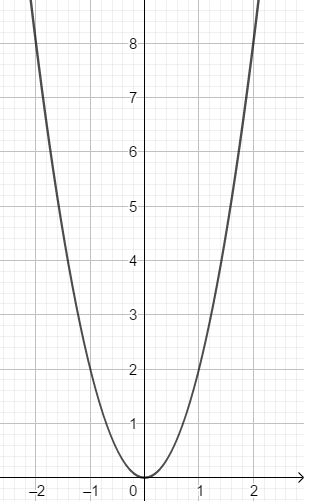
b) Vì \(K\left(\sqrt{2};4\right)\) thuộc parabol (P) nên \(4=a\left(\sqrt{2}\right)^2\Leftrightarrow a=2\)
Vậy phương trình parabol cần tìm là: \(y=2x^2\)
Bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 8 | 2 | 0 | 2 | 8 |

Câu 1:
a,Bạn tự vẽ
b,Phương trình hoành độ giao điểm của (d1) và (d2) là:
\(\(\(-2x+3=x-1\Rightarrow-3x=-4\Rightarrow x=\frac{4}{3}\)\)\)
\(\(\(\Rightarrow y=\frac{4}{3}-1=\frac{1}{3}\)\)\)
Vậy tọa độ giao điểm của (d1) và (d2) là \(\(\(\left(\frac{4}{3};\frac{1}{3}\right)\)\)\)
c,Đường thẳng (d3) có dạng: y = ax + b
Vì (d3) song song với (d1) \(\(\(\Rightarrow\hept{\begin{cases}a=a'\\b\ne b'\end{cases}}\Rightarrow\hept{\begin{cases}a=-2\\b\ne3\end{cases}}\)\)\)
Khi đó (d3) có dạng: y = -2x + b
Vì (d3) đi qua điểm A( -2 ; 1) nên \(\(\(\Rightarrow x=-2;y=1\)\)\)
Thay x = -2 ; y = 1 vào (d3) ta được:\(\(\(1=-2.\left(-2\right)+b\Rightarrow b=-3\)\)\)
Vậy (d3) có phương trình: y = -2x - 3
Câu 2:
\(A=\frac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\frac{1}{\sqrt{a}-\sqrt{b}}\left(a>0;b>0;a\ne b\right)\)(Đề chắc phải như này)
\(\(\(=\frac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}.\frac{\sqrt{a}-\sqrt{b}}{1}\)\)\)
\(\(\(=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)\)\)\)
\(\(\(=\sqrt{a}^2-\sqrt{b}^2\)\)\)
\(\(\(=a-b\)\)\)

Nè bạn :)
Ta có : \(2ab+2ac\ge4a\sqrt{bc}\) (Cauchy_)
\(\Rightarrow a^2+2ab+2ac+4bc\ge a^2+4a\sqrt{bc}+4bc\)
\(\Rightarrow a^2+2ab+2ac+4bc\ge\left(a+2\sqrt{bc}\right)^2\)
\(\Rightarrow\sqrt{\left(a+2b\right)\left(a+2c\right)}\ge a+2\sqrt{bc}\)\(\left(1\right)\)
Tương tự : \(\sqrt{\left(b+2a\right)\left(b+2c\right)}\ge b+2\sqrt{ac}\)\(\left(2\right)\)
\(\sqrt{\left(c+2a\right)\left(c+2b\right)}\ge c+2\sqrt{ab}\)\(\left(3\right)\)
Từ \(\left(1\right);\left(2\right);\left(3\right)\)\(\Rightarrow\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2\ge3\)
\(\Rightarrow\sqrt{a}+\sqrt{b}+\sqrt{c}\ge\sqrt{3}\)
Đẳng thức xảy ra khi \(a=b=c=\frac{1}{\sqrt{3}}\)
Thay vào biểu thức M ta được M = \(\frac{\sqrt{3}}{3}\)
Thay \(x=\sqrt{2},y=4-\sqrt{2}\) vào đồ thị ta có pt: \(\sqrt{2}a+b=4-\sqrt{2}\)
Thay \(x=2,y=\sqrt{2}\) vào đồ thị ta có pt: \(2a+b=\sqrt{2}\)
Ta có hpt: \(\left\{{}\begin{matrix}\sqrt{2}a+b=4-\sqrt{2}\\2a+b=\sqrt{2}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=4+\sqrt{2}\end{matrix}\right.\)