Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(\overrightarrow{a}+\overrightarrow{b}\right)^2=\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)\)\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2+2\overrightarrow{a}\overrightarrow{b}\).
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)\)\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2-2\overrightarrow{a}\overrightarrow{b}\).
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)=\left|\overrightarrow{a}\right|^2+\overrightarrow{a}\overrightarrow{b}-\overrightarrow{a}\overrightarrow{b}+\left|\overrightarrow{b}\right|^2\)\(=\left|\overrightarrow{a}\right|^2-\left|\overrightarrow{b}\right|^2\).

A={\(\frac{1}{x^2}\)x={1;2;3;.....;15}}
B={x+a I a={1;3;5;7;.....} ; x2=a1+x1;x3=a3+x3....}

Dựa vào tính chất :x<y và y<z thì x<z, ta có :
-12/-37<0 và 0< 13/38
=> -12/-37<13/38
Chúc bạn học tốt!
Ta có: \(\frac{13}{38}>\frac{13}{39}=\frac{1}{3}\) (1)
\(\frac{-12}{-37}=\frac{12}{37}< \frac{12}{36}=\frac{1}{3}\) (2)
Từ (1)(2) => \(\frac{13}{38}>\frac{-12}{-37}\)
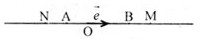
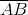 = 3;
= 3; 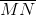 = -5. Từ đây ta có
= -5. Từ đây ta có 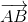 = 3
= 3 ,
, 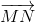 = -5
= -5
- Các tính chất của bất đẳng thức:
TC1. ( Tính chất bắc cầu)
TC2. (Quy tắc cộng)
A < B <=> A + C < B + C
TC3. (Quy tắc cộng hai bất đẳng thức dùng chiều)
TC4. (Quy tắc nhân)
TC5. (Quy tắc nhân hai bất đẳng thức)
TC6. (Quy tắc lũy thừa, khai căn)
Với A, B > 0, n ∈ N* ta có:
A < B <=> An < Bn
A < B <=>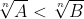 .
.
- Áp dụng tính chất: 0 < an < bn với n ∈ N*
Xét: 23000 = (23)1000
32000 = (32)1000
Ta có: 0<23<32 ⇒ (23)1000 < (32)1000
Do đó: 23000 < 32000