cho tam giác ABC , tia phân giác của góc ABC cắt AC tại D, chứng minh BD2=AB.BC-AD.DC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


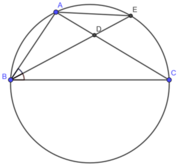
Gọi E là giao điểm của tia BD với đường tròn ngoại tiếp tam giác ABC.


A B C D E
Kẻ tia Cx sao cho \(\widehat{ABD}=\widehat{ACx}\). Tia Cx cắt BD tại E
+ ΔABD ∼ ΔECD ( g.g )
\(\Rightarrow\left\{{}\begin{matrix}\frac{AD}{BD}=\frac{ED}{CD}\\\widehat{BAD}=\widehat{CEB}\end{matrix}\right.\)
=> \(AD\cdot CD=BD\cdot ED\) (1)
+ ΔABD ∼ ΔEBC ( g.g )
\(\Rightarrow\frac{AB}{BD}=\frac{EB}{BC}\Rightarrow AB\cdot BC=BD\cdot EB\) (2)
+ Từ (1) và (2) suy ra : \(AB\cdot BC-AD\cdot CD=BD\cdot EB-BD\cdot ED=BD^2\)

A B C H D b a
Vì câu a dễ nên mik chỉ làm câu b thôi nhé --hơi dài đấy , cần kiên nhẫn đọc--hoặc tham khảo cách nào ngắn gọn hơn cũng được , hình chỉ minh họa , độ chính xác ko cao
====================
Kẻ BH là đường cao của tam giác ABC
\(\Delta BAD\) cân tại B ( BA=BD) có BH là đường cao nên cũng là đường trung tuyến
=> AH = \(\frac{AD}{2}\)
\(\Delta ABC\) có BD là đường phân giác trong nên : \(\frac{DA}{DC}=\frac{AB}{BC}=\frac{b}{a}\)
=>\(\frac{DA}{b}=\frac{DC}{a}=\frac{DA+DC}{a+b}=\frac{AC}{a+b}=\frac{b}{a+b}\)=> \(DA=\frac{b^2}{a+b}\)
\(\Delta HAB\) vuông tại H , theo định lí Pi - ta - go ta có :
AB2 = BH2 + AH2 => BH2 = AB2 -AH2 = \(b^2-\frac{AD^2}{4}\) (1)
\(\Delta HBC\) vuông tại H , theo định lí Pi-ta-go , ta suy ra :
BH2 = BC2 - HC2 = BC2 - (AC - AH)2 = \(a^2-\left(b-\frac{AD}{2}\right)^2\)= \(a^2-b^2+b.AD-\frac{AD^2}{4}\left(2\right)\)
Từ (1) và (2) ta suy ra :
\(b^2-\frac{AD^2}{4}\) = \(a^2-b^2+b.AD-\frac{AD^2}{4}\left(2\right)\)
<=> \(b^2-a^2=b.AD-b^2\)
<=>\(\left(b-a\right)\left(b+a\right)=b.\frac{b^2}{a+b}-b^2\)
<=>\(\left(b-a\right)\left(b+a\right)=\frac{-ab^2}{a+b}\)
<=>\(\frac{a-b}{ab}=\frac{b}{\left(a+b\right)^2}\)
<=>\(\frac{1}{a}-\frac{1}{b}=\frac{b}{\left(a+b\right)^2}\) (đpcm)
Sao cách của bn giống hệt sách kẻ thêm hình phụ của nguyễn đức tấn nhỉ :)))

a.TG ABC cân tại A gt
=> ^B = ^C tính chất tg cân
Mà ^ECB=^ACE=1/2^C ( CE là pg ^C)
^DBC=^ABD=1/2^B ( BD là pg ^B)
=> ^ECB=^ACE =^DBC=^ABD
Xét tg BEC và tg CDB có:
^ECB = ^DBC(cmt)
BC chung
^B=^C (tg ABC cân tại A)
=>tg BEC = tg CDB(g-c-g)
b. Xét tg ABD và tg ACE có
^A chung
AB = AC (tg ABC cân tại A)
^ABD=^ACE(cmt)
=>tg ABD = tg ACE(g-c-g)
=>AD=AE (cctu)
=> tg ADE là tg cân
A B C D E
Kẻ tia Cx sao cho \(\widehat{ABD}=\widehat{ACx}\) . Tia Cx cắt BD tại E
+ \(\Delta ABD~\Delta ECD\left(g.g\right)\)
\(\Rightarrow\hept{\begin{cases}\frac{AD}{BD}=\frac{ED}{CD}\\\widehat{BAD}=\widehat{CEB}\end{cases}}\)
\(\Rightarrow AD.CD=BD.ED\left(1\right)\)
+ \(\Delta ABD~\Delta EBC\left(g.g\right)\)
\(\Rightarrow\frac{AB}{BD}=\frac{EB}{BC}\Rightarrow AB.BC=EB.BD\left(2\right)\)
Từ (1) và (2) suy ra
\(AB.BC-AD.DC=BD.EB-BD.ED=BD^2\)