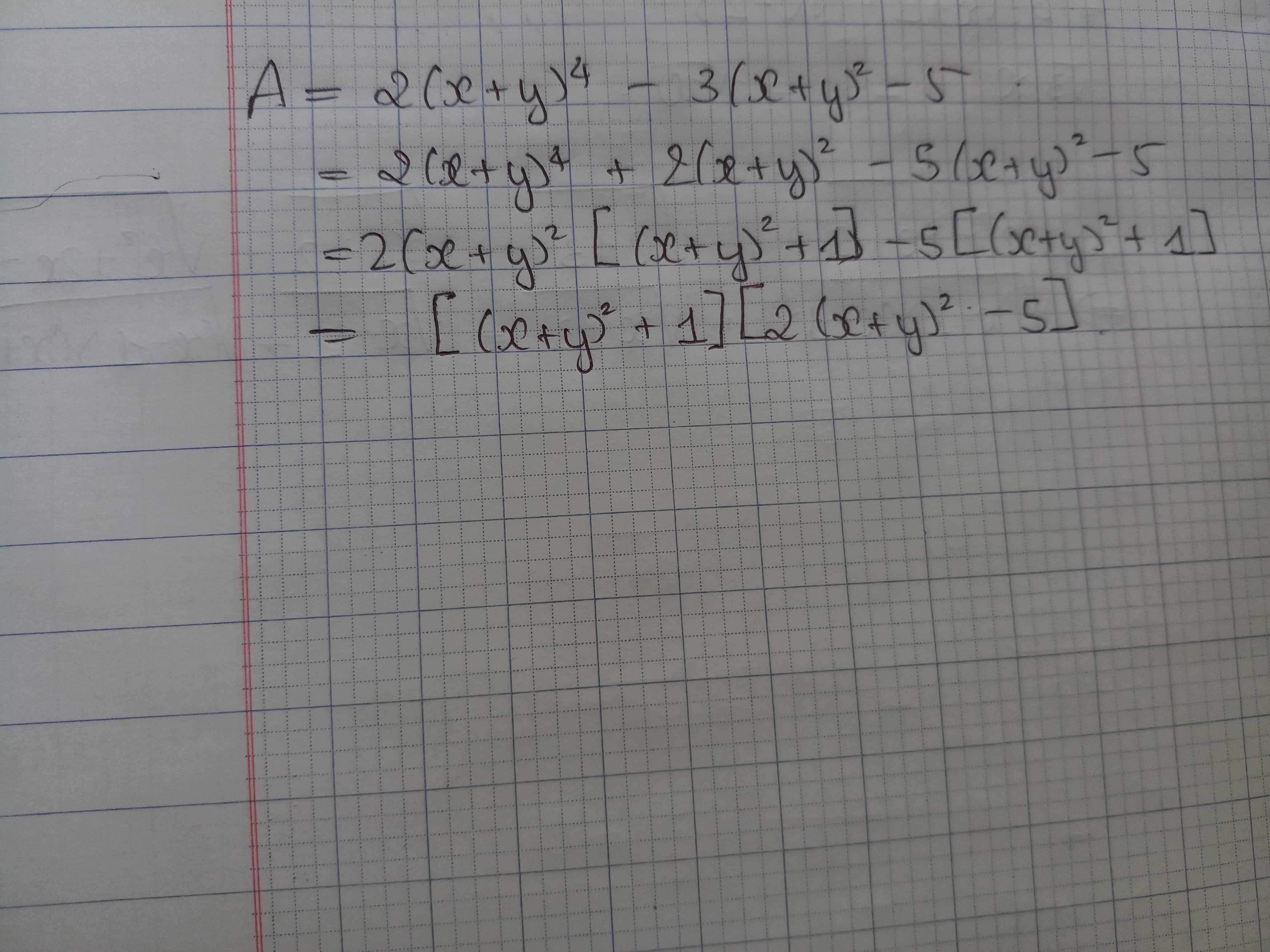giúp với pt đt thành nhân thức
giúp với pt đt thành nhân thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


6x2+7x-3
=6x2-2x+9x-3
=(6x2-2x)+(9x-3)
=2x(3x-1)+3(3x-1)
=(3x-1)(2x+3)

a, Gọi pt đường thẳng (d1) có dạng là y = ax + b
Do (d1) có tung độ gốc bằng 10
=>b = 10
=> (d1) y = ax + 10
Vì (d1) // (d) => a = a' và b khác b'
<=> a = 4 và 10 khác 0 (Luôn đúng)
=> (d1) y = 4x + 10
b,Gọi pt đường thằng (d2) là y = mx + n
Vì (d2) vuông với (d) nên \(4m=-1\Leftrightarrow m=-\frac{1}{4}\)
\(\Rightarrow\left(d_2\right)y=-\frac{1}{4}x+n\)
Vì (d2) cắt trục Ox tại điểm có hoành độ bằng 8 nên (d2) đi qua điểm (8;0)
Khi đó \(0=-\frac{1}{4}.8+n\)
\(\Leftrightarrow n=2\)
\(\Rightarrow\left(d_2\right)y=-\frac{1}{4}x+2\)

a) \(x^2-2xy+y^2-xz+yz\)
= \(\left(x-y\right)^2-z\left(x-y\right)\)
= \(\left(x-y\right)\left(x-y-z\right)\)
b) \(x^3+9x^2-4x-36\)
= \(x^3-2x^2+11x^2-22x+18x-36\)
= \(x^2\left(x-2\right)+11x\left(x-2\right)+18\left(x-2\right)\)
= \(\left(x-2\right)\left(x^2+11x+18\right)\)
= \(\left(x-2\right)\left(x^2+2x+9x+18\right)\)
= \(\left(x-2\right)\left(x+2\right)\left(x+9\right)\)
Chuc ban hoc tot

x^8+x+1= (x^8 - x^5) + (x^5 - x^2) + (x^2+x+1)
= x^5.(x^3-1) + x^2.(x^3-1) + (x^2+x+1)
= x^5.(x-1).(x^2+x+1) + x^2.(x-1).(x^2+x+1) + (x^2+x+1)
=(x^2+x+1).[x^5.(x-1)+x^2.(x-1)+1]

b) \(\dfrac{2}{3}x^2y-2xy^2+4xy=2xy\left(\dfrac{1}{3}x-y+2\right)\)
c) \(4x^2-2x-3y-9y^2\)
\(=\left(2x-3y\right)\left(2x+3y\right)-\left(2x+3y\right)\)
\(=\left(2x+3y\right)\left(2x-3y-1\right)\)

Ta có: \(A=2\left(x+y\right)^4-3\left(x+y\right)^2-5\)
\(=2\left(x+y\right)^4-5\left(x+y\right)^2+2\left(x+y\right)^2-5\)
\(=\left(x+y\right)^2\left[2\left(x+y\right)^2-5\right]+\left[2\left(x+y\right)^2-5\right]\)
\(=\left[2\left(x+y\right)^2-5\right]\left[\left(x+y\right)^2+1\right]\)

Gọi hàm số cần tìm có dạng y= ax+b
Xét phương trình hoành độ giao điểm của đồ thị 2 hàm số: y= 2x+1 và y= 3x-4
\(2x+1=3x-4\)
\(\Leftrightarrow x=5\Rightarrow y=2.5+1=11\)
\(\Rightarrow\left(5;11\right)\)
Vì đồ thị hàm số y= ax+b // với đường thẳng: \(y=\sqrt{2}x+15\Rightarrow a=\sqrt{2}\)
Thay vào hàm số:
\(\sqrt{2}.5+b=11\Rightarrow b=11-5\sqrt{2}\)
\(\Rightarrow y=\sqrt{2}x+11-5\sqrt{2}\)
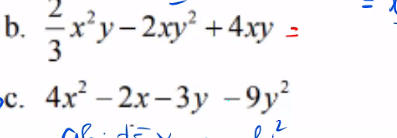 phân tích các đt trên thành nhân tử ::>>>
phân tích các đt trên thành nhân tử ::>>>