Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Charlie và Elly ngồi cạnh nhau, Anna và Daniel ko ngồi cạnh nhau mà chỉ có 5 người:
=> Anna hoặc Daniel sẽ ngồi cạnh Charlie hoặc Elly => Bella chỉ có thể ngồi giữa Anna và Daniel.
Tính sin2a, cos2a, tan2a, biết:
a) sina = -0,6 và π < a <
#Hỏi cộng đồng OLM
#Mẫu giáo
a) π < a < => sina < 0, cosa < 0, tana > 0
sin2a = 2sinacosa = 2(-0,6)(-) = 0,96
cos2a = cos2 a – sin2 a = 1 – 2sin2 a = 1 - 0,72 = 0,28
tan2a = ≈ 3,1286
b) < a < π => sina > 0, cosa < 0
sina =
sin2a = 2sinacosa = 2.
cos2a = 2cos2a - 1 = 2 - 1 = -
tan2a =
c) < a < π =>
< 2a < 2π => sin2a < 0, cos2a > 0, tan2a < 0
sin2a = - 1 = -0,75
cos2a =
tan2a = -
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt
#Hỏi cộng đồng OLM
#Mẫu giáo
a) Hoành độ điểm P là :
xp = OP = OM. cos α = R.cosα
Phương trình đường thẳng OM là y = tanα.x. Thể tích V của khối tròn xoay là:
b) Đặt t = cosα => t ∈ . (vì α ∈
), α = arccos t.
Ta có :
V' = 0 ⇔
hoặc (loại).
Ta có bảng biến thiên:
Từ đó suy ra V(t) lớn nhất ⇔ , khi đó :
.
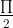< a < π => sina > 0, cosa < 0
cos2a =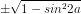 
= ±
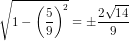
Nếu cos2a =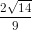 
thì
sina =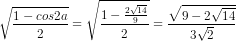 
= 
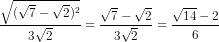
cosa = -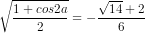
Nếu cos2a = -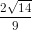 thì
sina =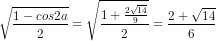 
cosa = -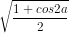
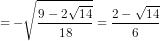
Chứng minh các bất đẳng thức sau:
a) tanx > x (0 < x <
#Hỏi cộng đồng OLM
#Mẫu giáo
a) Xét hàm số y = f(x) = tanx – x với x ∈ [0 ; ).
Ta có : y’ = - 1 ≥ 0, x ∈ [0 ;
); y’ = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ;
).
Từ đó ∀x ∈ (0 ; ) thì f(x) > f(0) ⇔ tanx – x > tan0 – 0 = 0 hay tanx > x.
b) Xét hàm số y = g(x) = tanx – x - . với x ∈ [0 ;
).
Ta có : y’ = - 1 - x2 = 1 + tan2x - 1 - x2 = tan2x - x2
= (tanx - x)(tanx + x), ∀x ∈ [0 ; ).
Vì ∀x ∈ [0 ; ) nên tanx + x ≥ 0 và tanx - x >0 (theo câu a).
Do đó y' ≥ 0, ∀x ∈ [0 ; ).
Dễ thấy y' = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ; ). Từ đó : ∀x ∈ [0 ;
) thì g(x) > g(0) ⇔ tanx – x -
> tan0 - 0 - 0 = 0 hay tanx > x +
.
dien a dang o mon toan lai sang mo anh do khung
Thì trả lời 0 được à ? Cần gì phải mắng mình như thế