I. Tính đơn điệu của hàm số
Hãy hoàn thành 2 câu hỏi dưới đây để nhớ lại kiến thức cũ đã học:
Cho đồ thị hàm số y=\cos xy=cosx như hình vẽ sau:

Hàm số giảm trong khoảng nào dưới đây?
(-\dfrac{\pi}{2};0)(−2π;0)
(\pi;\dfrac{3\pi}{2})(π;23π)
(-\dfrac{\pi}{2};\dfrac{\pi}{2})(−2π;2π)
Kiểm tra
1. Định nghĩa:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y=f\left(x\right)y=f(x) xác định trên K. Ta nói
Hàm số y=f\left(x\right)y=f(x) đồng biến (tăng) trên KK nếu với mọi cặp x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)< f\left(x_2\right)f(x1)<f(x2);
Hàm số y=f\left(x\right)y=f(x) nghịch biến (giảm) trên KK nếu với mọi cặp mà x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)>f\left(x_2\right)f(x1)>f(x2).
Hàm số đồng biến hoặc nghịch biến trên KK được gọi chung là hàm số đơn điệu trên KK.
Nhận xét: Từ định nghĩa trên ta thấy:
a) f\left(x\right)f(x) đồng biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)>0,∀x1,x2∈K (x_1\ne x_2x1=x2);
f\left(x\right)f(x) nghịch biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}< 0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)<0,∀x1,x2∈K (x_1\ne x_2x1=x2).
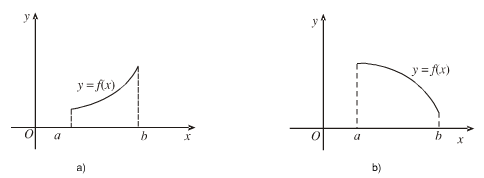
b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải (hình a);
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải (hình b).
2) Tính đơn điệu và dấu của đạo hàm
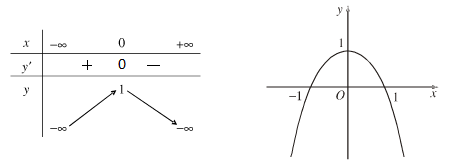
Cho hàm số y=-\dfrac{x^2}{2}y=−2x2 với đồ thị như sau. Hàm số có đạo hàm y'=-xy′=−x.

Trên khoảng \left(-\infty;0\right)(−∞;0) đạo hàm mang dấu dươngâm , hàm số đồng biếnnghịch biến.
Trên khoảng \left(0;+\infty\right)(0;+∞) đạo hàm mang dấu dươngâm, hàm số đồng biếnnghịch biến.
Kiểm tra
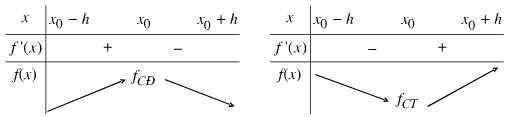
Định lý: Cho hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K.
a) Nếu f'\left(x\right)>0f′(x)>0 với mọi xx thuộc K thì hàm số f\left(x\right)f(x) đồng biến trên K.
b) Nếu f'\left(x\right)< 0f′(x)<0 với mọi xx thuộc K thì hàm số nghịch biến trên K.
Xét hàm số y=\sin xy=sinx trên khoảng \left(0;2\pi\right)(0;2π) có đạo hàm và bảng biến thiên như sau:

Hàm số y=\sin xy=sinx đồng biến trên những khoảng nào dưới đây?
\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)(2π;23π)
\left(0;\dfrac{3\pi}{2}\right)(0;23π)
\left(0;\dfrac{\pi}{2}\right)(0;2π)
\left(\dfrac{3\pi}{2};2\pi\right)(23π;2π)
Kiểm tra
Định lý mở rộng: Giả sử hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K. Nếu f'\left(x\right)\ge0f′(x)≥0 (hoặc f'\left(x\right)\le0f′(x)≤0), \forall x\in K∀x∈K và f'\left(x\right)=0f′(x)=0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (hoặc nghịch biến) trên K.
Ví dụ: hàm số y=2x^3+6x^2+6x-7y=2x3+6x2+6x−7 có đạo hàm y'=6x^2+12x+6=6\left(x+1\right)^2\ge0,\forall x\in\mathbb{R}y′=6x2+12x+6=6(x+1)2≥0,∀x∈R. Vậy hàm số đồng biến trên \mathbb{R}R.
II. Qui tắc xét tính đơn điệu của hàm số
Qui tắc:
1. Tìm tập xác định
2. Tính đạo f'\left(x\right)f′(x). Tìm các điểm x_1,x_2,...,x_nx1,x2,...,xn mà tại đó đạo hàm bằng 0 hoặc không xác định.
3. Sắp xếp các điểm x_1,x_2,...,x_nx1,x2,...,xn theo thứ tự tăng dần và lập bảng biến thiên.
4. Rút ra kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Xét sự đồng biến, nghịch biến của hàm số y=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2-2x+2y=31x3−21x2−2x+2.
1) Tập xác định: \mathbb{R}R.
2) y'=x^2-x-2y′=x2−x−2, y'=0\Leftrightarrow\left[{}\begin{aligned}x=-1\\x=2\end{aligned}\right.y′=0⇔[x=−1x=2
3) Bảng biến thiên
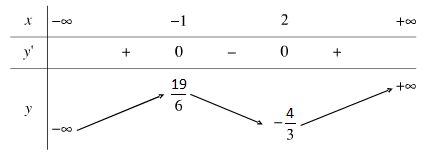
4) Rút ra kết luận:
Hàm số đồng biếnnghịch biến trên các khoảng \left(-\infty;-1\right)(−∞;−1) và \left(2;+\infty\right)(2;+∞).
Hàm số đồng biếnnghịch biến trên khoản \left(-1;2\right)(−1;2).
sdddssKiểm tra
I. Tính đơn điệu của hàm số
Hãy hoàn thành 2 câu hỏi dưới đây để nhớ lại kiến thức cũ đã học:
Cho đồ thị hàm số y=\cos xy=cosx như hình vẽ sau:

Hàm số giảm trong khoảng nào dưới đây?
(-\dfrac{\pi}{2};0)(−2π;0)
(\pi;\dfrac{3\pi}{2})(π;23π)
(-\dfrac{\pi}{2};\dfrac{\pi}{2})(−2π;2π)
Kiểm tra
1. Định nghĩa:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y=f\left(x\right)y=f(x) xác định trên K. Ta nói
Hàm số y=f\left(x\right)y=f(x) đồng biến (tăng) trên KK nếu với mọi cặp x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)< f\left(x_2\right)f(x1)<f(x2);
Hàm số y=f\left(x\right)y=f(x) nghịch biến (giảm) trên KK nếu với mọi cặp mà x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)>f\left(x_2\right)f(x1)>f(x2).
Hàm số đồng biến hoặc nghịch biến trên KK được gọi chung là hàm số đơn điệu trên KK.
Nhận xét: Từ định nghĩa trên ta thấy:
a) f\left(x\right)f(x) đồng biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)>0,∀x1,x2∈K (x_1\ne x_2x1=x2);
f\left(x\right)f(x) nghịch biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}< 0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)<0,∀x1,x2∈K (x_1\ne x_2x1=x2).
b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải (hình a);
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải (hình b).

2) Tính đơn điệu và dấu của đạo hàm
Cho hàm số y=-\dfrac{x^2}{2}y=−2x2 với đồ thị như sau. Hàm số có đạo hàm y'=-xy′=−x.

Trên khoảng \left(-\infty;0\right)(−∞;0) đạo hàm mang dấu dươngâm , hàm số đồng biếnnghịch biến.
Trên khoảng \left(0;+\infty\right)(0;+∞) đạo hàm mang dấu dươngâm, hàm số đồng biếnnghịch biến.
Kiểm tra
Định lý: Cho hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K.
a) Nếu f'\left(x\right)>0f′(x)>0 với mọi xx thuộc K thì hàm số f\left(x\right)f(x) đồng biến trên K.
b) Nếu f'\left(x\right)< 0f′(x)<0 với mọi xx thuộc K thì hàm số nghịch biến trên K.
Xét hàm số y=\sin xy=sinx trên khoảng \left(0;2\pi\right)(0;2π) có đạo hàm và bảng biến thiên như sau:

Hàm số y=\sin xy=sinx đồng biến trên những khoảng nào dưới đây?
\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)(2π;23π)
\left(0;\dfrac{3\pi}{2}\right)(0;23π)
\left(0;\dfrac{\pi}{2}\right)(0;2π)
\left(\dfrac{3\pi}{2};2\pi\right)(23π;2π)
Kiểm tra
Định lý mở rộng: Giả sử hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K. Nếu f'\left(x\right)\ge0f′(x)≥0 (hoặc f'\left(x\right)\le0f′(x)≤0), \forall x\in K∀x∈K và f'\left(x\right)=0f′(x)=0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (hoặc nghịch biến) trên K.
Ví dụ: hàm số y=2x^3+6x^2+6x-7y=2x3+6x2+6x−7 có đạo hàm y'=6x^2+12x+6=6\left(x+1\right)^2\ge0,\forall x\in\mathbb{R}y′=6x2+12x+6=6(x+1)2≥0,∀x∈R. Vậy hàm số đồng biến trên \mathbb{R}R.
II. Qui tắc xét tính đơn điệu của hàm số
Qui tắc:
1. Tìm tập xác định
2. Tính đạo f'\left(x\right)f′(x). Tìm các điểm x_1,x_2,...,x_nx1,x2,...,xn mà tại đó đạo hàm bằng 0 hoặc không xác định.
3. Sắp xếp các điểm x_1,x_2,...,x_nx1,x2,...,xn theo thứ tự tăng dần và lập bảng biến thiên.
4. Rút ra kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Xét sự đồng biến, nghịch biến của hàm số y=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2-2x+2y=31x3−21x2−2x+2.
1) Tập xác định: \mathbb{R}R.
2) y'=x^2-x-2y′=x2−x−2, y'=0\Leftrightarrow\left[{}\begin{aligned}x=-1\\x=2\end{aligned}\right.y′=0⇔[x=−1x=2
3) Bảng biến thiên

4) Rút ra kết luận:
Hàm số đồng biếnnghịch biến trên các khoảng \left(-\infty;-1\right)(−∞;−1) và \left(2;+\infty\right)(2;+∞).
Hàm số đồng biếnnghịch biến trên khoản \left(-1;2\right)(−1;2).
Kiểm tra
I. Tính đơn điệu của hàm số
Hãy hoàn thành 2 câu hỏi dưới đây để nhớ lại kiến thức cũ đã học:
Cho đồ thị hàm số y=\cos xy=cosx như hình vẽ sau:

Hàm số giảm trong khoảng nào dưới đây?
(-\dfrac{\pi}{2};0)(−2π;0)
(\pi;\dfrac{3\pi}{2})(π;23π)
(-\dfrac{\pi}{2};\dfrac{\pi}{2})(−2π;2π)
Kiểm tra
1. Định nghĩa:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y=f\left(x\right)y=f(x) xác định trên K. Ta nói
Hàm số y=f\left(x\right)y=f(x) đồng biến (tăng) trên KK nếu với mọi cặp x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)< f\left(x_2\right)f(x1)<f(x2);
Hàm số y=f\left(x\right)y=f(x) nghịch biến (giảm) trên KK nếu với mọi cặp mà x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)>f\left(x_2\right)f(x1)>f(x2).
Hàm số đồng biến hoặc nghịch biến trên KK được gọi chung là hàm số đơn điệu trên KK.
Nhận xét: Từ định nghĩa trên ta thấy:
a) f\left(x\right)f(x) đồng biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)>0,∀x1,x2∈K (x_1\ne x_2x1=x2);
f\left(x\right)f(x) nghịch biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}< 0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)<0,∀x1,x2∈K (x_1\ne x_2x1=x2).
b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải (hình a);
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải (hình b).

2) Tính đơn điệu và dấu của đạo hàm
Cho hàm số y=-\dfrac{x^2}{2}y=−2x2 với đồ thị như sau. Hàm số có đạo hàm y'=-xy′=−x.

Trên khoảng \left(-\infty;0\right)(−∞;0) đạo hàm mang dấu dươngâm , hàm số đồng biếnnghịch biến.
Trên khoảng \left(0;+\infty\right)(0;+∞) đạo hàm mang dấu dươngâm, hàm số đồng biếnnghịch biến.
Kiểm tra
Định lý: Cho hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K.
a) Nếu f'\left(x\right)>0f′(x)>0 với mọi xx thuộc K thì hàm số f\left(x\right)f(x) đồng biến trên K.
b) Nếu f'\left(x\right)< 0f′(x)<0 với mọi xx thuộc K thì hàm số nghịch biến trên K.
Xét hàm số y=\sin xy=sinx trên khoảng \left(0;2\pi\right)(0;2π) có đạo hàm và bảng biến thiên như sau:

Hàm số y=\sin xy=sinx đồng biến trên những khoảng nào dưới đây?
\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)(2π;23π)
\left(0;\dfrac{3\pi}{2}\right)(0;23π)
\left(0;\dfrac{\pi}{2}\right)(0;2π)
\left(\dfrac{3\pi}{2};2\pi\right)(23π;2π)
Kiểm tra
Định lý mở rộng: Giả sử hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K. Nếu f'\left(x\right)\ge0f′(x)≥0 (hoặc f'\left(x\right)\le0f′(x)≤0), \forall x\in K∀x∈K và f'\left(x\right)=0f′(x)=0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (hoặc nghịch biến) trên K.
Ví dụ: hàm số y=2x^3+6x^2+6x-7y=2x3+6x2+6x−7 có đạo hàm y'=6x^2+12x+6=6\left(x+1\right)^2\ge0,\forall x\in\mathbb{R}y′=6x2+12x+6=6(x+1)2≥0,∀x∈R. Vậy hàm số đồng biến trên \mathbb{R}R.
II. Qui tắc xét tính đơn điệu của hàm số
Qui tắc:
1. Tìm tập xác định
2. Tính đạo f'\left(x\right)f′(x). Tìm các điểm x_1,x_2,...,x_nx1,x2,...,xn mà tại đó đạo hàm bằng 0 hoặc không xác định.
3. Sắp xếp các điểm x_1,x_2,...,x_nx1,x2,...,xn theo thứ tự tăng dần và lập bảng biến thiên.
4. Rút ra kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Xét sự đồng biến, nghịch biến của hàm số y=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2-2x+2y=31x3−21x2−2x+2.
1) Tập xác định: \mathbb{R}R.
2) y'=x^2-x-2y′=x2−x−2, y'=0\Leftrightarrow\left[{}\begin{aligned}x=-1\\x=2\end{aligned}\right.y′=0⇔[x=−1x=2
3) Bảng biến thiên

4) Rút ra kết luận:
Hàm số đồng biếnnghịch biến trên các khoảng \left(-\infty;-1\right)(−∞;−1) và \left(2;+\infty\right)(2;+∞).
Hàm số đồng biếnnghịch biến trên khoản \left(-1;2\right)(−1;2).
Kiểm tra
I. Tính đơn điệu của hàm số
Hãy hoàn thành 2 câu hỏi dưới đây để nhớ lại kiến thức cũ đã học:
Cho đồ thị hàm số y=\cos xy=cosx như hình vẽ sau:

Hàm số giảm trong khoảng nào dưới đây?
(-\dfrac{\pi}{2};0)(−2π;0)
(\pi;\dfrac{3\pi}{2})(π;23π)
(-\dfrac{\pi}{2};\dfrac{\pi}{2})(−2π;2π)
Kiểm tra
1. Định nghĩa:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y=f\left(x\right)y=f(x) xác định trên K. Ta nói
Hàm số y=f\left(x\right)y=f(x) đồng biến (tăng) trên KK nếu với mọi cặp x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)< f\left(x_2\right)f(x1)<f(x2);
Hàm số y=f\left(x\right)y=f(x) nghịch biến (giảm) trên KK nếu với mọi cặp mà x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)>f\left(x_2\right)f(x1)>f(x2).
Hàm số đồng biến hoặc nghịch biến trên KK được gọi chung là hàm số đơn điệu trên KK.
Nhận xét: Từ định nghĩa trên ta thấy:
a) f\left(x\right)f(x) đồng biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)>0,∀x1,x2∈K (x_1\ne x_2x1=x2);
f\left(x\right)f(x) nghịch biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}< 0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)<0,∀x1,x2∈K (x_1\ne x_2x1=x2).
b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải (hình a);
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải (hình b).

2) Tính đơn điệu và dấu của đạo hàm
Cho hàm số y=-\dfrac{x^2}{2}y=−2x2 với đồ thị như sau. Hàm số có đạo hàm y'=-xy′=−x.

Trên khoảng \left(-\infty;0\right)(−∞;0) đạo hàm mang dấu dươngâm , hàm số đồng biếnnghịch biến.
Trên khoảng \left(0;+\infty\right)(0;+∞) đạo hàm mang dấu dươngâm, hàm số đồng biếnnghịch biến.
Kiểm tra
Định lý: Cho hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K.
a) Nếu f'\left(x\right)>0f′(x)>0 với mọi xx thuộc K thì hàm số f\left(x\right)f(x) đồng biến trên K.
b) Nếu f'\left(x\right)< 0f′(x)<0 với mọi xx thuộc K thì hàm số nghịch biến trên K.
Xét hàm số y=\sin xy=sinx trên khoảng \left(0;2\pi\right)(0;2π) có đạo hàm và bảng biến thiên như sau:

Hàm số y=\sin xy=sinx đồng biến trên những khoảng nào dưới đây?
\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)(2π;23π)
\left(0;\dfrac{3\pi}{2}\right)(0;23π)
\left(0;\dfrac{\pi}{2}\right)(0;2π)
\left(\dfrac{3\pi}{2};2\pi\right)(23π;2π)
Kiểm tra
Định lý mở rộng: Giả sử hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K. Nếu f'\left(x\right)\ge0f′(x)≥0 (hoặc f'\left(x\right)\le0f′(x)≤0), \forall x\in K∀x∈K và f'\left(x\right)=0f′(x)=0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (hoặc nghịch biến) trên K.
Ví dụ: hàm số y=2x^3+6x^2+6x-7y=2x3+6x2+6x−7 có đạo hàm y'=6x^2+12x+6=6\left(x+1\right)^2\ge0,\forall x\in\mathbb{R}y′=6x2+12x+6=6(x+1)2≥0,∀x∈R. Vậy hàm số đồng biến trên \mathbb{R}R.
II. Qui tắc xét tính đơn điệu của hàm số
Qui tắc:
1. Tìm tập xác định
2. Tính đạo f'\left(x\right)f′(x). Tìm các điểm x_1,x_2,...,x_nx1,x2,...,xn mà tại đó đạo hàm bằng 0 hoặc không xác định.
3. Sắp xếp các điểm x_1,x_2,...,x_nx1,x2,...,xn theo thứ tự tăng dần và lập bảng biến thiên.
4. Rút ra kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Xét sự đồng biến, nghịch biến của hàm số y=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2-2x+2y=31x3−21x2−2x+2.
1) Tập xác định: \mathbb{R}R.
2) y'=x^2-x-2y′=x2−x−2, y'=0\Leftrightarrow\left[{}\begin{aligned}x=-1\\x=2\end{aligned}\right.y′=0⇔[x=−1x=2
3) Bảng biến thiên

4) Rút ra kết luận:
Hàm số đồng biếnnghịch biến trên các khoảng \left(-\infty;-1\right)(−∞;−1) và \left(2;+\infty\right)(2;+∞).
Hàm số đồng biếnnghịch biến trên khoản \left(-1;2\right)(−1;2).
Kiểm tra
I. Tính đơn điệu của hàm số
Hãy hoàn thành 2 câu hỏi dưới đây để nhớ lại kiến thức cũ đã học:
Cho đồ thị hàm số y=\cos xy=cosx như hình vẽ sau:

Hàm số giảm trong khoảng nào dưới đây?
(-\dfrac{\pi}{2};0)(−2π;0)
(\pi;\dfrac{3\pi}{2})(π;23π)
(-\dfrac{\pi}{2};\dfrac{\pi}{2})(−2π;2π)
Kiểm tra
1. Định nghĩa:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y=f\left(x\right)y=f(x) xác định trên K. Ta nói
Hàm số y=f\left(x\right)y=f(x) đồng biến (tăng) trên KK nếu với mọi cặp x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)< f\left(x_2\right)f(x1)<f(x2);
Hàm số y=f\left(x\right)y=f(x) nghịch biến (giảm) trên KK nếu với mọi cặp mà x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)>f\left(x_2\right)f(x1)>f(x2).
Hàm số đồng biến hoặc nghịch biến trên KK được gọi chung là hàm số đơn điệu trên KK.
Nhận xét: Từ định nghĩa trên ta thấy:
a) f\left(x\right)f(x) đồng biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)>0,∀x1,x2∈K (x_1\ne x_2x1=x2);
f\left(x\right)f(x) nghịch biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}< 0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)<0,∀x1,x2∈K (x_1\ne x_2x1=x2).
b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải (hình a);
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải (hình b).

2) Tính đơn điệu và dấu của đạo hàm
Cho hàm số y=-\dfrac{x^2}{2}y=−2x2 với đồ thị như sau. Hàm số có đạo hàm y'=-xy′=−x.

Trên khoảng \left(-\infty;0\right)(−∞;0) đạo hàm mang dấu dươngâm , hàm số đồng biếnnghịch biến.
Trên khoảng \left(0;+\infty\right)(0;+∞) đạo hàm mang dấu dươngâm, hàm số đồng biếnnghịch biến.
Kiểm tra
Định lý: Cho hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K.
a) Nếu f'\left(x\right)>0f′(x)>0 với mọi xx thuộc K thì hàm số f\left(x\right)f(x) đồng biến trên K.
b) Nếu f'\left(x\right)< 0f′(x)<0 với mọi xx thuộc K thì hàm số nghịch biến trên K.
Xét hàm số y=\sin xy=sinx trên khoảng \left(0;2\pi\right)(0;2π) có đạo hàm và bảng biến thiên như sau:

Hàm số y=\sin xy=sinx đồng biến trên những khoảng nào dưới đây?
\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)(2π;23π)
\left(0;\dfrac{3\pi}{2}\right)(0;23π)
\left(0;\dfrac{\pi}{2}\right)(0;2π)
\left(\dfrac{3\pi}{2};2\pi\right)(23π;2π)
Kiểm tra
Định lý mở rộng: Giả sử hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K. Nếu f'\left(x\right)\ge0f′(x)≥0 (hoặc f'\left(x\right)\le0f′(x)≤0), \forall x\in K∀x∈K và f'\left(x\right)=0f′(x)=0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (hoặc nghịch biến) trên K.
Ví dụ: hàm số y=2x^3+6x^2+6x-7y=2x3+6x2+6x−7 có đạo hàm y'=6x^2+12x+6=6\left(x+1\right)^2\ge0,\forall x\in\mathbb{R}y′=6x2+12x+6=6(x+1)2≥0,∀x∈R. Vậy hàm số đồng biến trên \mathbb{R}R.
II. Qui tắc xét tính đơn điệu của hàm số
Qui tắc:
1. Tìm tập xác định
2. Tính đạo f'\left(x\right)f′(x). Tìm các điểm x_1,x_2,...,x_nx1,x2,...,xn mà tại đó đạo hàm bằng 0 hoặc không xác định.
3. Sắp xếp các điểm x_1,x_2,...,x_nx1,x2,...,xn theo thứ tự tăng dần và lập bảng biến thiên.
4. Rút ra kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Xét sự đồng biến, nghịch biến của hàm số y=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2-2x+2y=31x3−21x2−2x+2.
1) Tập xác định: \mathbb{R}R.
2) y'=x^2-x-2y′=x2−x−2, y'=0\Leftrightarrow\left[{}\begin{aligned}x=-1\\x=2\end{aligned}\right.y′=0⇔[x=−1x=2
3) Bảng biến thiên

4) Rút ra kết luận:
Hàm số đồng biếnnghịch biến trên các khoảng \left(-\infty;-1\right)(−∞;−1) và \left(2;+\infty\right)(2;+∞).
Hàm số đồng biếnnghịch biến trên khoản \left(-1;2\right)(−1;2).
Kiểm tra
I. Tính đơn điệu của hàm số
Hãy hoàn thành 2 câu hỏi dưới đây để nhớ lại kiến thức cũ đã học:
Cho đồ thị hàm số y=\cos xy=cosx như hình vẽ sau:

Hàm số giảm trong khoảng nào dưới đây?
(-\dfrac{\pi}{2};0)(−2π;0)
(\pi;\dfrac{3\pi}{2})(π;23π)
(-\dfrac{\pi}{2};\dfrac{\pi}{2})(−2π;2π)
Kiểm tra
1. Định nghĩa:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y=f\left(x\right)y=f(x) xác định trên K. Ta nói
Hàm số y=f\left(x\right)y=f(x) đồng biến (tăng) trên KK nếu với mọi cặp x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)< f\left(x_2\right)f(x1)<f(x2);
Hàm số y=f\left(x\right)y=f(x) nghịch biến (giảm) trên KK nếu với mọi cặp mà x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)>f\left(x_2\right)f(x1)>f(x2).
Hàm số đồng biến hoặc nghịch biến trên KK được gọi chung là hàm số đơn điệu trên KK.
Nhận xét: Từ định nghĩa trên ta thấy:
a) f\left(x\right)f(x) đồng biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)>0,∀x1,x2∈K (x_1\ne x_2x1=x2);
f\left(x\right)f(x) nghịch biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}< 0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)<0,∀x1,x2∈K (x_1\ne x_2x1=x2).
b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải (hình a);
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải (hình b).

2) Tính đơn điệu và dấu của đạo hàm
Cho hàm số y=-\dfrac{x^2}{2}y=−2x2 với đồ thị như sau. Hàm số có đạo hàm y'=-xy′=−x.

Trên khoảng \left(-\infty;0\right)(−∞;0) đạo hàm mang dấu dươngâm , hàm số đồng biếnnghịch biến.
Trên khoảng \left(0;+\infty\right)(0;+∞) đạo hàm mang dấu dươngâm, hàm số đồng biếnnghịch biến.
Kiểm tra
Định lý: Cho hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K.
a) Nếu f'\left(x\right)>0f′(x)>0 với mọi xx thuộc K thì hàm số f\left(x\right)f(x) đồng biến trên K.
b) Nếu f'\left(x\right)< 0f′(x)<0 với mọi xx thuộc K thì hàm số nghịch biến trên K.
Xét hàm số y=\sin xy=sinx trên khoảng \left(0;2\pi\right)(0;2π) có đạo hàm và bảng biến thiên như sau:

Hàm số y=\sin xy=sinx đồng biến trên những khoảng nào dưới đây?
\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)(2π;23π)
\left(0;\dfrac{3\pi}{2}\right)(0;23π)
\left(0;\dfrac{\pi}{2}\right)(0;2π)
\left(\dfrac{3\pi}{2};2\pi\right)(23π;2π)
Kiểm tra
Định lý mở rộng: Giả sử hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K. Nếu f'\left(x\right)\ge0f′(x)≥0 (hoặc f'\left(x\right)\le0f′(x)≤0), \forall x\in K∀x∈K và f'\left(x\right)=0f′(x)=0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (hoặc nghịch biến) trên K.
Ví dụ: hàm số y=2x^3+6x^2+6x-7y=2x3+6x2+6x−7 có đạo hàm y'=6x^2+12x+6=6\left(x+1\right)^2\ge0,\forall x\in\mathbb{R}y′=6x2+12x+6=6(x+1)2≥0,∀x∈R. Vậy hàm số đồng biến trên \mathbb{R}R.
II. Qui tắc xét tính đơn điệu của hàm số
Qui tắc:
1. Tìm tập xác định
2. Tính đạo f'\left(x\right)f′(x). Tìm các điểm x_1,x_2,...,x_nx1,x2,...,xn mà tại đó đạo hàm bằng 0 hoặc không xác định.
3. Sắp xếp các điểm x_1,x_2,...,x_nx1,x2,...,xn theo thứ tự tăng dần và lập bảng biến thiên.
4. Rút ra kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Xét sự đồng biến, nghịch biến của hàm số y=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2-2x+2y=31x3−21x2−2x+2.
1) Tập xác định: \mathbb{R}R.
2) y'=x^2-x-2y′=x2−x−2, y'=0\Leftrightarrow\left[{}\begin{aligned}x=-1\\x=2\end{aligned}\right.y′=0⇔[x=−1x=2
3) Bảng biến thiên

4) Rút ra kết luận:
Hàm số đồng biếnnghịch biến trên các khoảng \left(-\infty;-1\right)(−∞;−1) và \left(2;+\infty\right)(2;+∞).
Hàm số đồng biếnnghịch biến trên khoản \left(-1;2\right)(−1;2).
Kiểm tra
I. Tính đơn điệu của hàm số
Hãy hoàn thành 2 câu hỏi dưới đây để nhớ lại kiến thức cũ đã học:
Cho đồ thị hàm số y=\cos xy=cosx như hình vẽ sau:

Hàm số giảm trong khoảng nào dưới đây?
(-\dfrac{\pi}{2};0)(−2π;0)
(\pi;\dfrac{3\pi}{2})(π;23π)
(-\dfrac{\pi}{2};\dfrac{\pi}{2})(−2π;2π)
Kiểm tra
1. Định nghĩa:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y=f\left(x\right)y=f(x) xác định trên K. Ta nói
Hàm số y=f\left(x\right)y=f(x) đồng biến (tăng) trên KK nếu với mọi cặp x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)< f\left(x_2\right)f(x1)<f(x2);
Hàm số y=f\left(x\right)y=f(x) nghịch biến (giảm) trên KK nếu với mọi cặp mà x_1,x_2\in Kx1,x2∈K mà x_1< x_2x1<x2 thì f\left(x_1\right)>f\left(x_2\right)f(x1)>f(x2).
Hàm số đồng biến hoặc nghịch biến trên KK được gọi chung là hàm số đơn điệu trên KK.
Nhận xét: Từ định nghĩa trên ta thấy:
a) f\left(x\right)f(x) đồng biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)>0,∀x1,x2∈K (x_1\ne x_2x1=x2);
f\left(x\right)f(x) nghịch biến trên KK \Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}< 0,\forall x_1,x_2\in K⇔x2−x1f(x2)−f(x1)<0,∀x1,x2∈K (x_1\ne x_2x1=x2).
b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải (hình a);
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải (hình b).

2) Tính đơn điệu và dấu của đạo hàm
Cho hàm số y=-\dfrac{x^2}{2}y=−2x2 với đồ thị như sau. Hàm số có đạo hàm y'=-xy′=−x.

Trên khoảng \left(-\infty;0\right)(−∞;0) đạo hàm mang dấu dươngâm , hàm số đồng biếnnghịch biến.
Trên khoảng \left(0;+\infty\right)(0;+∞) đạo hàm mang dấu dươngâm, hàm số đồng biếnnghịch biến.
Kiểm tra
Định lý: Cho hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K.
a) Nếu f'\left(x\right)>0f′(x)>0 với mọi xx thuộc K thì hàm số f\left(x\right)f(x) đồng biến trên K.
b) Nếu f'\left(x\right)< 0f′(x)<0 với mọi xx thuộc K thì hàm số nghịch biến trên K.
Xét hàm số y=\sin xy=sinx trên khoảng \left(0;2\pi\right)(0;2π) có đạo hàm và bảng biến thiên như sau:

Hàm số y=\sin xy=sinx đồng biến trên những khoảng nào dưới đây?
\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)(2π;23π)
\left(0;\dfrac{3\pi}{2}\right)(0;23π)
\left(0;\dfrac{\pi}{2}\right)(0;2π)
\left(\dfrac{3\pi}{2};2\pi\right)(23π;2π)
Kiểm tra
Định lý mở rộng: Giả sử hàm số y=f\left(x\right)y=f(x) có đạo hàm trên K. Nếu f'\left(x\right)\ge0f′(x)≥0 (hoặc f'\left(x\right)\le0f′(x)≤0), \forall x\in K∀x∈K và f'\left(x\right)=0f′(x)=0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (hoặc nghịch biến) trên K.
Ví dụ: hàm số y=2x^3+6x^2+6x-7y=2x3+6x2+6x−7 có đạo hàm y'=6x^2+12x+6=6\left(x+1\right)^2\ge0,\forall x\in\mathbb{R}y′=6x2+12x+6=6(x+1)2≥0,∀x∈R. Vậy hàm số đồng biến trên \mathbb{R}R.
II. Qui tắc xét tính đơn điệu của hàm số
Qui tắc:
1. Tìm tập xác định
2. Tính đạo f'\left(x\right)f′(x). Tìm các điểm x_1,x_2,...,x_nx1,x2,...,xn mà tại đó đạo hàm bằng 0 hoặc không xác định.
3. Sắp xếp các điểm x_1,x_2,...,x_nx1,x2,...,xn theo thứ tự tăng dần và lập bảng biến thiên.
4. Rút ra kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Xét sự đồng biến, nghịch biến của hàm số y=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2-2x+2y=31x3−21x2−2x+2.
1) Tập xác định: \mathbb{R}R.
2) y'=x^2-x-2y′=x2−x−2, y'=0\Leftrightarrow\left[{}\begin{aligned}x=-1\\x=2\end{aligned}\right.y′=0⇔[x=−1x=2
3) Bảng biến thiên

4) Rút ra kết luận:
Hàm số đồng biếnnghịch biến trên các khoảng \left(-\infty;-1\right)(−∞;−1) và \left(2;+\infty\right)(2;+∞).
Hàm số đồng biếnnghịch biến trên khoản \left(-1;2\right)(−1;2).
Kiểm tra