TM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LM
3
KH
23 tháng 5 2017
..
x3 + y3 + 3xy = x3 + y3 + 3xy(x + y) (vì x + y = 1)
= x3 + 3x2y + 3xy2 + y3
= (x + y)3
= 13 = 1.
ý b tương tự.
TC
27 tháng 8 2017
tuổi con HN là :
50 : ( 1 + 4 ) = 10 ( tuổi )
tuổi bố HN là :
50 - 10 = 40 ( tuổi )
hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi
ta có sơ đồ : bố : |----|----|----|
con : |----| hiệu 30 tuổi
tuổi con khi đó là :
30 : ( 3 - 1 ) = 15 ( tuổi )
số năm mà bố gấp 3 tuổi con là :
15 - 10 = 5 ( năm )
ĐS : 5 năm
mình nha
H
2
24 tháng 7 2018
\(Q=x^3-y^3-3xy\)
\(\Rightarrow Q=\left(x-y\right)\left(x^2+xy+y^2\right)-3xy\)
\(\Rightarrow Q=x^2+xy+y^2-3xy\)
\(\Rightarrow Q=x^2-2xy+y^2=\left(x-y\right)^2\)
\(\Rightarrow Q=1^2=1\)
DT
2
7 tháng 10 2016
Phan Văn Hiếu Bài của bạn ngay từ dòng đầu đã sai hướng làm rồi nhé :)
Ta có :
\(x^3+y^3+3xy\)
\(=\left(x^3+3x^2y+3xy^2+y^3\right)+3xy-3x^2y-3xy^2\)
\(=\left(x+y\right)^3-3xy\left(x+y-1\right)\)
Thay \(x+y=1;\) có :
\(=1^3-3xy\left(1-1\right)\)
\(=1-0\)
\(=1\)
Vậy ...
7 tháng 10 2016
\(x^3+y^3+3xy=\left(x+y\right)\left(x^2+xy+y^2\right)+3xy\)
\(=x^2+2xy+y^2+2xy\)
\(=2xy\)
đế đây mk chịu
KT
1 tháng 10 2016
a)\(\left(x+y\right)^3=x^3+y^3+3xy\left(x+y\right)=x^3+y^3+3xy=1^3=1\)
b)\(\left(x-y\right)^3=x^3-y^3-3xy\left(x-y\right)=x^3-y^3-3xy=1^3=1\)
Bài này là trên vio mk cx gặp r
TT
0
LG
1
28 tháng 6 2016
\(M=x^3-3xy\left(x-y\right)-y^3-x^2+2xy-y^2\)
\(=x^3-3x^2y+3xy^2-y^3-x^2+2xy-y^2\)
\(=\left(x-y\right)^3-\left(x-y\right)^2\)
\(=x-y\)
\(=7\)
L
1
30 tháng 11 2019
a)\(A=\left(\frac{x+y}{x-2y}+\frac{3y}{2y-x}-3xy\right).\frac{x+1}{3xy-1}+\frac{x^2}{x+1}\)
\(=\left(\frac{x+y-3y}{x-2y}-3xy\right).\frac{x+1}{3xy-1}+\frac{x^2}{x+1}\)
\(=\left(\frac{x-2y}{x-2y}-3xy\right).\frac{x+1}{3xy-1}+\frac{x^2}{x+1}\)
\(=\left(1-3xy\right).\frac{-x-1}{1-3xy}+\frac{x^2}{x+1}\)
\(=-\left(x+1\right)+\frac{x^2}{x+1}\)`
\(=\frac{-\left(x+1\right)^2+x^2}{x+1}\)
\(=\frac{-x^2-2x-1+x^2}{x+1}\)
\(=\frac{-2x-1}{x+1}\)(1)
b) Thay \(x=-3,y=2014\)vào (1) ta được:
\(A=\frac{-2.\left(-3\right)-1}{-3+1}=\frac{-5}{2}\)
Vậy \(A=\frac{-5}{2}\)với x=-3 và y=2014
NT
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
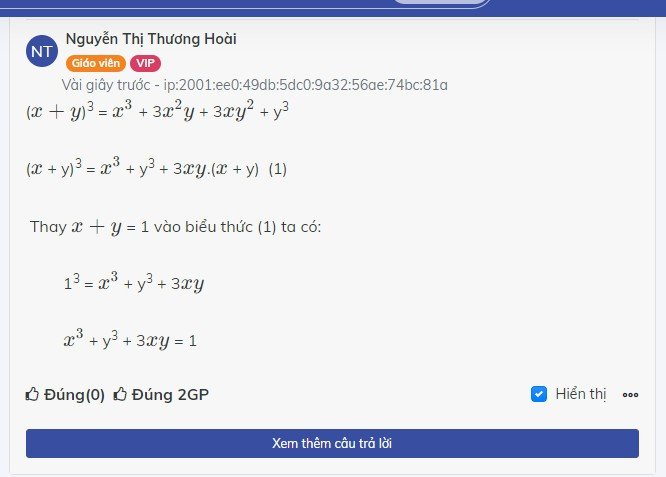
Ta có
\(\left(x+x\right)^3=x^3+3x^2y+3xy^2+y^3=x^3+y^3+3xy\left(x+y\right)\)
\(\Rightarrow x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\)
\(\Rightarrow K=\left(x+y\right)^3-3xy\left(x+y\right)+3xy\) Với x+y=1
\(\Rightarrow K=1^3-3xy+3xy=1\)