
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4*cos(pi/6-a)*sin(pi/3-a)
=4*(cospi/6*cosa+sinpi/6*sina)*(sinpi/3*cosa-sina*cospi/3)
=4*(căn 3/2*cosa+1/2*sina)*(căn 3/2*cosa-1/2*sina)
=4*(3/4*cos^2a-1/4*sin^2a)
=3cos^2a-sin^2a
=3(1-sin^2a)-sin^2a
=3-4sin^2a
=>m=3; n=-4
m^2-n^2=-7

Ta có:
\(\dfrac{1}{cos^2x-sin^2x}+\dfrac{2tanx}{1-tan^2x}=\dfrac{1}{cos2x}+tan2x=\dfrac{1}{cos2x}+\dfrac{sin2x}{cos2x}=\dfrac{1+sin2x}{cos2x}=\dfrac{cos2x}{1-sin2x}\)
\(\Rightarrow P=a+b=2+1=3\)

23:
u4=10 và u7=22
=>\(\left\{{}\begin{matrix}u1+3d=10\\u1+6d=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3d=-12\\u1+3d=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}d=4\\u1=10-12=-2\end{matrix}\right.\)
=>Chọn C
Câu 22:
\(\left\{{}\begin{matrix}u1+2u5=0\\S_4=14\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u1+2\left(u1+4d\right)=0\\4\cdot\dfrac{\left[2u1+3d\right]}{2}=14\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3u1+8d=0\\2u1+3d=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6u1+16d=0\\6u1+9d=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7d=-21\\2u_1+3d=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=-3\\2u_1=7-3d=7+9=16\end{matrix}\right.\)
=>\(u_1=8;d=-3\)
=>Chọn A
21A
19B



a, \(f\left(x\right)=2x^4-x^3+4x^2-x\)
\(\Rightarrow f'\left(x\right)=\left(2x^4-x^3+4x^2-x\right)'\)
\(=\left(2x^4\right)'-\left(x^3\right)'+\left(4x^2\right)'-\left(x\right)'\)
\(=2.4x^3-3x^2+4.2x-1\)
\(=8x^3-3x^2+8x-1\)
b, \(f\left(x\right)=2sinx\)
\(\Rightarrow f'\left(x\right)=\left(2sinx\right)'=2cosx\)
c, \(f\left(x\right)=\dfrac{3x^2+2x-5}{x}\)
\(\Rightarrow f'\left(x\right)=\left(\dfrac{3x^2+2x-5}{x}\right)'\)
\(=\left(3x+2-\dfrac{5}{x}\right)'\)
\(=\left(3x\right)'+\left(2\right)'-\left(\dfrac{5}{x}\right)'\)
\(=3+0+\dfrac{5}{x^2}=\dfrac{5}{x^2}+3\)

a.
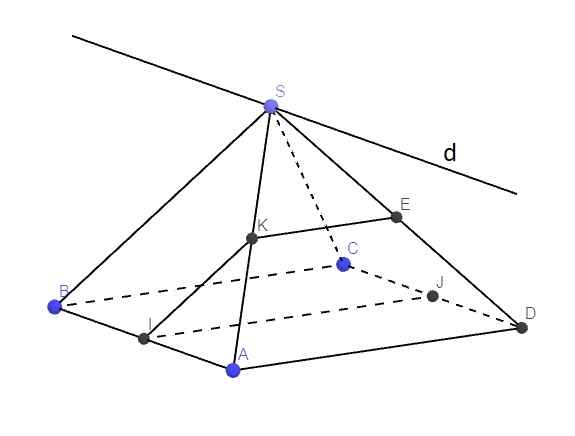
Do S là 1 điểm chung của (SAB), (SCD) đồng thời \(AB||CD\Rightarrow\) giao tuyến của (SAB) và (SCD) sẽ qua S và song song AB, CD
Qua S kẻ đường thẳng \(d||AB\)
\(\Rightarrow d=\left(SAB\right)\cap\left(SCD\right)\)
b.
Do I là trung điểm AB, J là trung điểm CD \(\Rightarrow IJ||BC||AD\) (đường trung bình hình bình hành)
Mà \(BC\in\left(SBC\right)\Rightarrow IJ||\left(SBD\right)\)
c.
Trong mp (SAD), qua K kẻ đường thẳng song song AD cắt SD tại E
\(\left\{{}\begin{matrix}K\in\left(IJK\right)\\KE||AD||IJ\end{matrix}\right.\) \(\Rightarrow KE\in\left(IJK\right)\Rightarrow E\in\left(IJK\right)\)
\(\Rightarrow E=SD\cap\left(IJK\right)\)

a) Có \(1\ge cosx\ge-1\)
\(\Leftrightarrow2\ge cosx+1\ge0\)
\(\Leftrightarrow\sqrt{2}\ge\sqrt{cosx+1}\ge0\)
\(\Leftrightarrow2\sqrt{2}-3\ge y\ge-3\)
\(miny=-3\Leftrightarrow cosx=-1\Leftrightarrow x=\pi+k2\pi\)
\(maxy=2\sqrt{2}-3\Leftrightarrow cosx=1\Leftrightarrow x=k2\pi\)
Vậy...
b) \(y=5\left(\dfrac{3}{5}sinx-\dfrac{4}{5}cosx\right)+2\)
Đặt \(cosu=\dfrac{3}{5}\Rightarrow sinu=\dfrac{4}{5}\)
\(y=5\left(sinx.cosu-cosx.sinu\right)+2\)
\(=5sin\left(x-u\right)+2\in\left[-3;7\right]\)
\(miny=-3\Leftrightarrow sin\left(x-u\right)=-1\Leftrightarrow x-u=-\dfrac{\pi}{2}+k2\pi\)\(\Leftrightarrow x=arccos\left(\dfrac{3}{5}\right)-\dfrac{\pi}{2}+k2\pi\)
\(maxy=7\Leftrightarrow sin\left(x-u\right)=1\Leftrightarrow x-u=\dfrac{\pi}{2}+k2\pi\)\(\Leftrightarrow x=acrcos\left(\dfrac{3}{5}\right)+\dfrac{\pi}{2}+k2\pi\)
c) Đặt \(t=sinx,t\in\left[-1;1\right]\)
\(y=4t^2-4t+3\)
\(y'=0\Leftrightarrow8t-4=0\Leftrightarrow t=\dfrac{1}{2}\)
Vẽ BBT, từ đó suy ra \(miny=2\Leftrightarrow t=\dfrac{1}{2}\Leftrightarrow sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\) ( k nguyên)
\(maxy=11\Leftrightarrow t=-1\Leftrightarrow sinx=-1\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\) ( k nguyên)
Vậy...
d)\(y=cos^2x+2sinx+2\)
\(=1-sin^2x+2sinx+2\)
\(=-sin^2x+2sinx+3\)
Đặt \(t=sinx,t\in\left[-1;1\right]\)
\(y=-t^2+2t+3\Rightarrow y'=0\Leftrightarrow t=1\)
Vẽ BBT, suy ra \(miny=0\Leftrightarrow t=-1\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(maxy=4\Leftrightarrow t=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
Vậy...
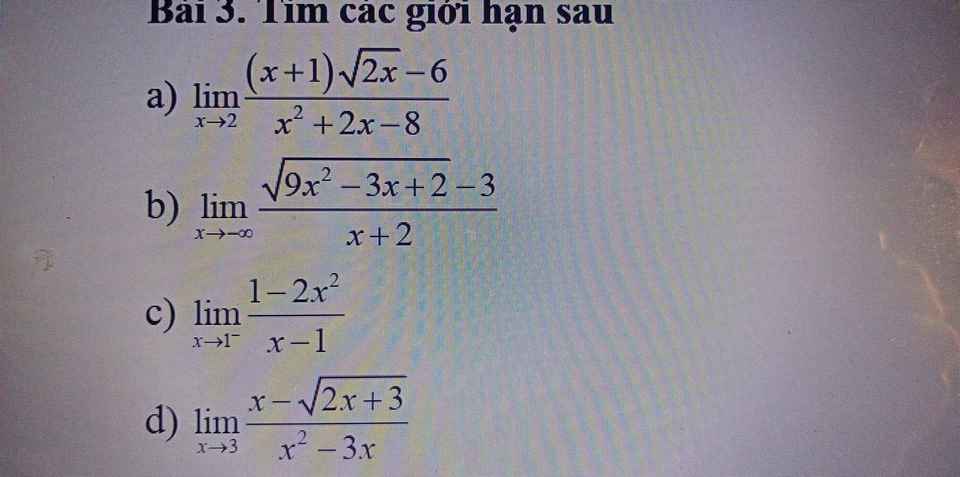
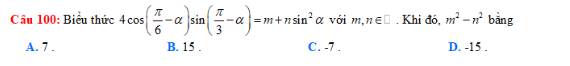
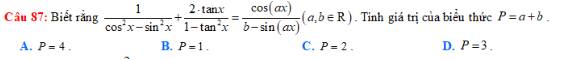


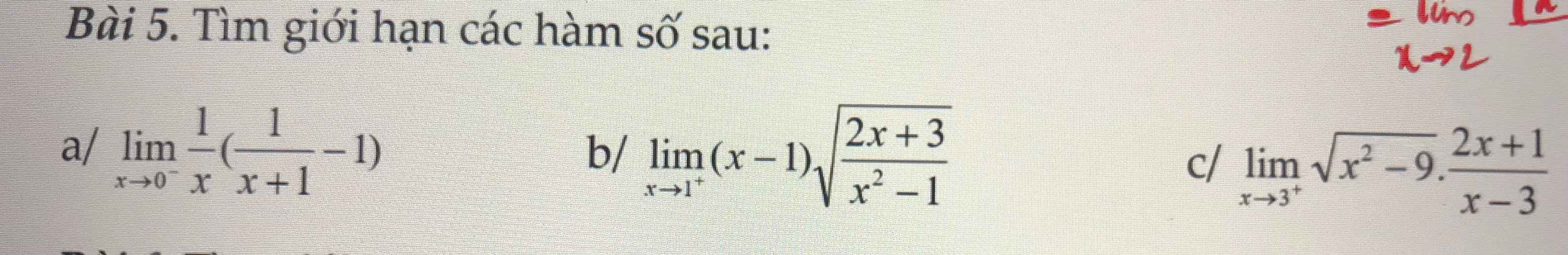
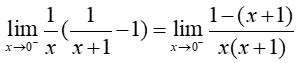
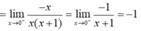
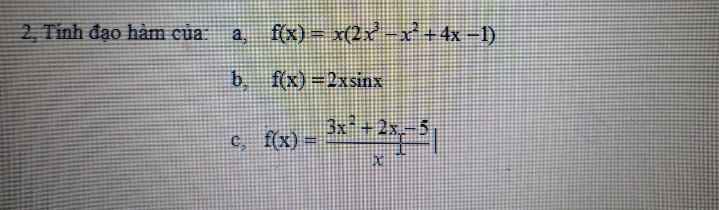

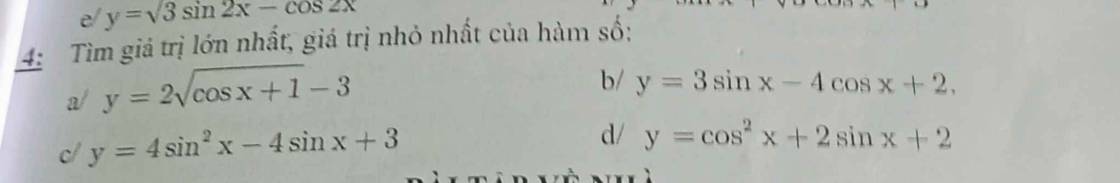
a.
\(\lim\limits_{x\rightarrow2}\dfrac{x\sqrt{2x}+\sqrt{2x}-6}{x^2+2x-8}=\lim\limits_{x\rightarrow2}\dfrac{\left(x\sqrt{2x}-4\right)+\left(\sqrt{2x}-2\right)}{\left(x-2\right)\left(x+4\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{2x^3-16}{x\sqrt{2x}+4}+\dfrac{2x-4}{\sqrt{2x}+2}}{\left(x-2\right)\left(x+4\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{2\left(x-2\right)\left(x^2+2x+4\right)}{x\sqrt{2x}+4}+\dfrac{2\left(x-2\right)}{\sqrt{2x}+2}}{\left(x-2\right)\left(x+4\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{2\left(x^2+2x+4\right)}{x\sqrt{2x}+4}+\dfrac{2}{\sqrt{2x}+2}}{x+4}\)
\(=\dfrac{\dfrac{2\left(2^2+2.2+4\right)}{2\sqrt{4}+4}+\dfrac{2}{\sqrt{4}+2}}{2+4}\)
\(=...\)
b.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{9x^2-3x+2}-3}{x+2}=\lim\limits_{x\rightarrow-\infty}\dfrac{\left|x\right|\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-3}{x+2}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-x\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-3}{x+2}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{x\left(-\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-\dfrac{3}{x}\right)}{x\left(1+\dfrac{2}{x}\right)}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-\dfrac{3}{x}}{1+\dfrac{2}{x}}\)
\(=\dfrac{-\sqrt{9-0+0}-0}{1+0}=...\)