K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2022
a.
\(\lim\limits_{x\rightarrow2}\dfrac{x\sqrt{2x}+\sqrt{2x}-6}{x^2+2x-8}=\lim\limits_{x\rightarrow2}\dfrac{\left(x\sqrt{2x}-4\right)+\left(\sqrt{2x}-2\right)}{\left(x-2\right)\left(x+4\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{2x^3-16}{x\sqrt{2x}+4}+\dfrac{2x-4}{\sqrt{2x}+2}}{\left(x-2\right)\left(x+4\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{2\left(x-2\right)\left(x^2+2x+4\right)}{x\sqrt{2x}+4}+\dfrac{2\left(x-2\right)}{\sqrt{2x}+2}}{\left(x-2\right)\left(x+4\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{2\left(x^2+2x+4\right)}{x\sqrt{2x}+4}+\dfrac{2}{\sqrt{2x}+2}}{x+4}\)
\(=\dfrac{\dfrac{2\left(2^2+2.2+4\right)}{2\sqrt{4}+4}+\dfrac{2}{\sqrt{4}+2}}{2+4}\)
\(=...\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2022
b.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{9x^2-3x+2}-3}{x+2}=\lim\limits_{x\rightarrow-\infty}\dfrac{\left|x\right|\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-3}{x+2}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-x\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-3}{x+2}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{x\left(-\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-\dfrac{3}{x}\right)}{x\left(1+\dfrac{2}{x}\right)}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-\dfrac{3}{x}}{1+\dfrac{2}{x}}\)
\(=\dfrac{-\sqrt{9-0+0}-0}{1+0}=...\)
BA
1
21 tháng 7 2023
4*cos(pi/6-a)*sin(pi/3-a)
=4*(cospi/6*cosa+sinpi/6*sina)*(sinpi/3*cosa-sina*cospi/3)
=4*(căn 3/2*cosa+1/2*sina)*(căn 3/2*cosa-1/2*sina)
=4*(3/4*cos^2a-1/4*sin^2a)
=3cos^2a-sin^2a
=3(1-sin^2a)-sin^2a
=3-4sin^2a
=>m=3; n=-4
m^2-n^2=-7
BA
1
20 tháng 7 2023
Ta có:
\(\dfrac{1}{cos^2x-sin^2x}+\dfrac{2tanx}{1-tan^2x}=\dfrac{1}{cos2x}+tan2x=\dfrac{1}{cos2x}+\dfrac{sin2x}{cos2x}=\dfrac{1+sin2x}{cos2x}=\dfrac{cos2x}{1-sin2x}\)
\(\Rightarrow P=a+b=2+1=3\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
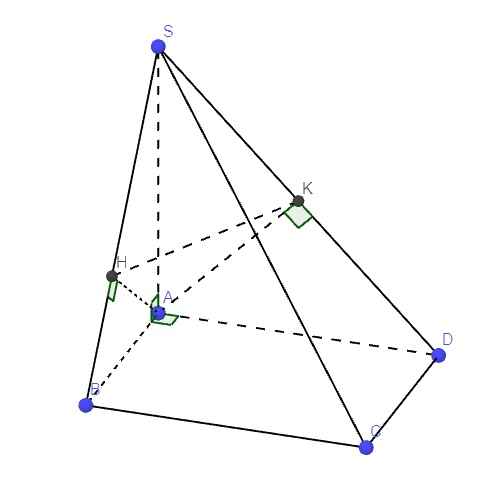
\(SA\perp\left(ABCD\right)\Rightarrow\left\{{}\begin{matrix}SA\perp AB\\SA\perp AD\end{matrix}\right.\) \(\Rightarrow\) các tam giác SAB và SAD vuông tại A
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\Rightarrow\Delta SBC\) vuông tại B
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\)
\(\Rightarrow\Delta SCD\) vuông tại D
b.
\(\left\{{}\begin{matrix}BC\perp\left(SAB\right)\Rightarrow BC\perp AH\\AH\perp SB\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\) (1)
\(\left\{{}\begin{matrix}CD\perp\left(SAD\right)\Rightarrow CD\perp AK\\AK\perp SD\end{matrix}\right.\) \(\Rightarrow AK\perp\left(SCD\right)\Rightarrow AK\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(AHK\right)\)
L
1
27 tháng 10 2023
23:
u4=10 và u7=22
=>\(\left\{{}\begin{matrix}u1+3d=10\\u1+6d=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3d=-12\\u1+3d=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}d=4\\u1=10-12=-2\end{matrix}\right.\)
=>Chọn C
Câu 22:
\(\left\{{}\begin{matrix}u1+2u5=0\\S_4=14\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u1+2\left(u1+4d\right)=0\\4\cdot\dfrac{\left[2u1+3d\right]}{2}=14\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3u1+8d=0\\2u1+3d=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6u1+16d=0\\6u1+9d=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7d=-21\\2u_1+3d=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=-3\\2u_1=7-3d=7+9=16\end{matrix}\right.\)
=>\(u_1=8;d=-3\)
=>Chọn A
21A
19B
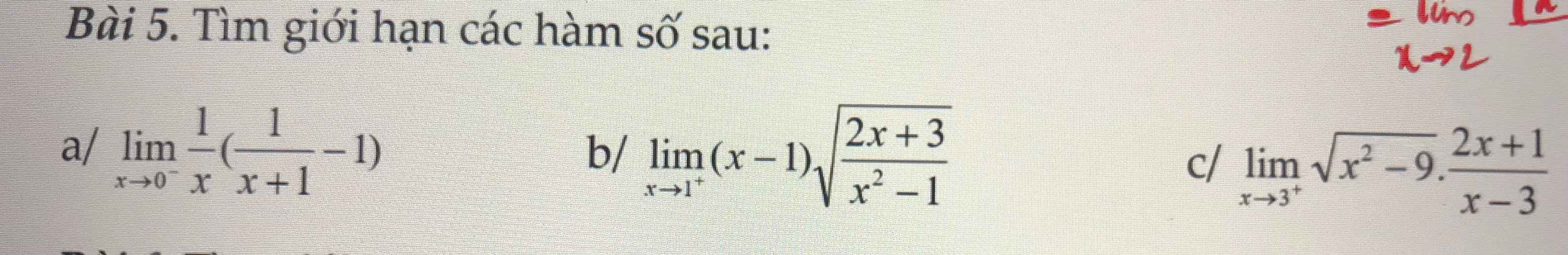
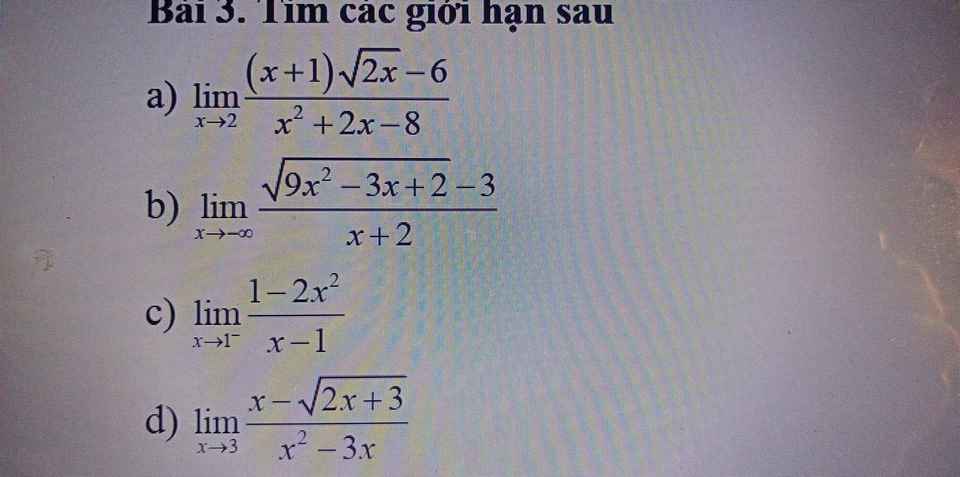
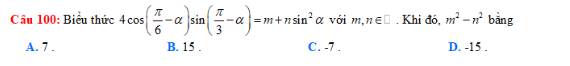
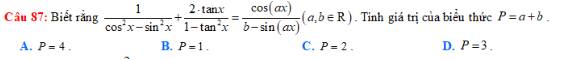
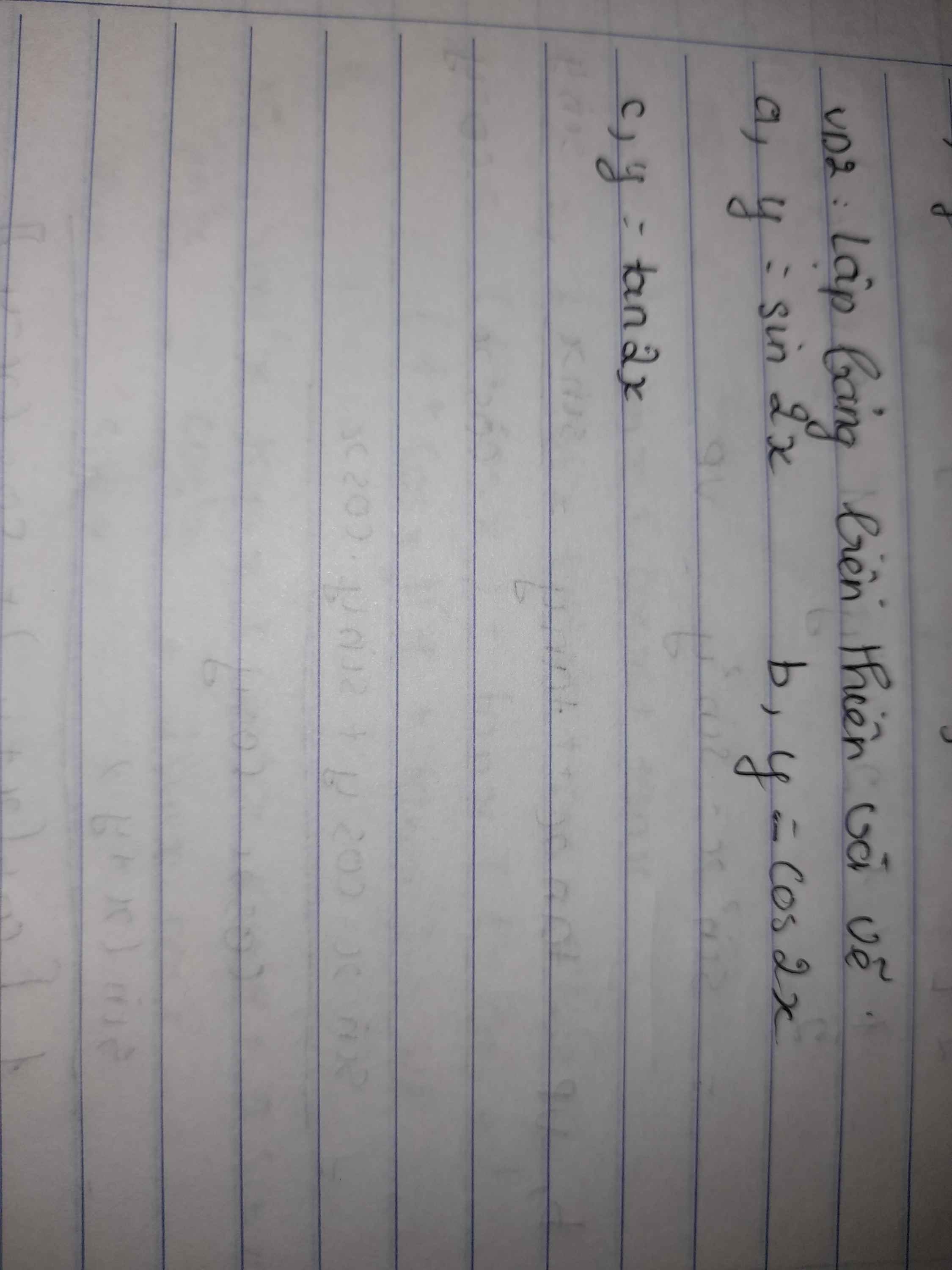
câu a / tham khảo:
Ta có:
có thể giải thích cho mik hiểu đk ko ạ chỗ quy đồng x+1 lên tử