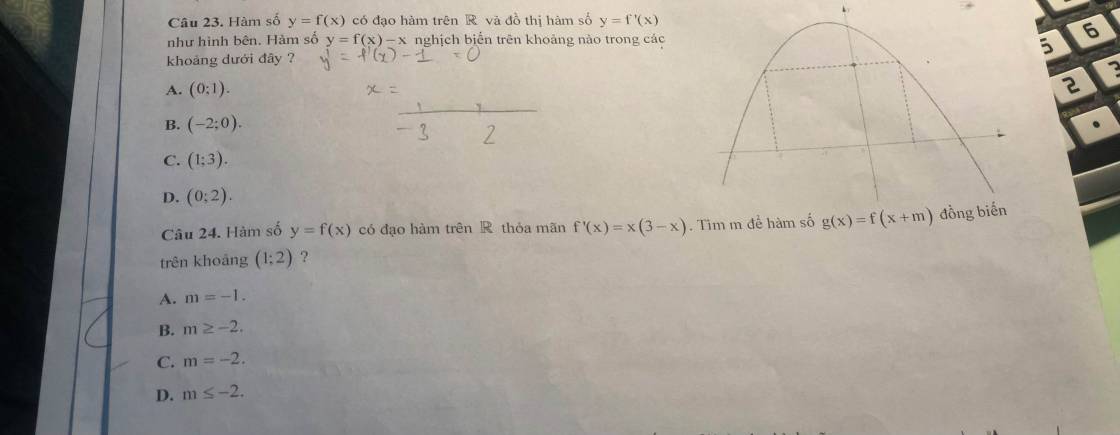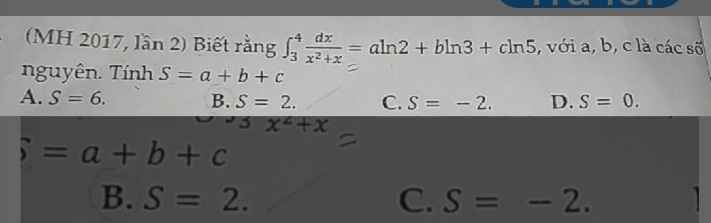K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 11 2021
12. \(\dfrac{4\sqrt{3}}{3}\pi\)
13. \(12\pi\)
14. \(\sqrt{6}\pi a^2\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 12 2022
42.
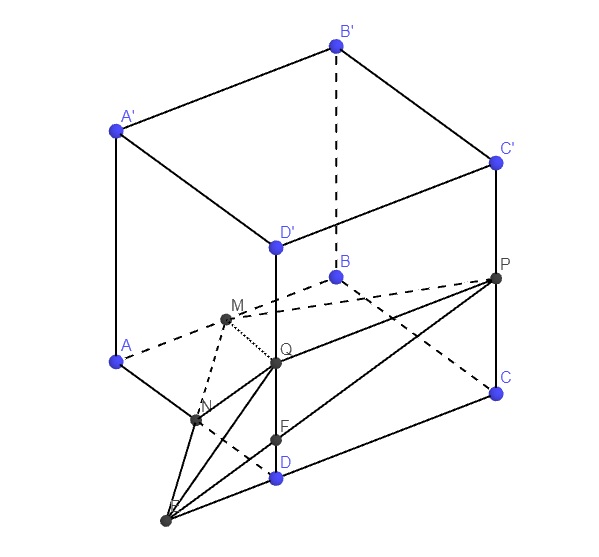
Do mọi hình hộp đều cho kết quả như nhau nên để đơn giản, chúng ta sẽ sử dụng hình hộp chữ nhật để tính toán (với 1 dạng hộp bất kì thì cần kẻ đường cao để tính tỉ lệ, như vậy rất mất thời gian, trong khi sử dụng hộp chữ nhật thì có thể sử dụng trực tiếp cạnh để tính, gọn hơn nhiều):
Nối MN kéo dài cắt CD tại E \(\Rightarrow AM=DE=\dfrac{1}{2}CD\)
Nối PE cắt D'D tại F \(\Rightarrow\dfrac{DF}{CP}=\dfrac{DE}{CE}=\dfrac{1}{3}\Rightarrow DF=\dfrac{1}{3}CP=\dfrac{1}{6}CC'\)
\(\Rightarrow QF=\dfrac{1}{2}CC'-\dfrac{1}{6}CC'=\dfrac{1}{3}CC'\)
\(V_{MNPQ}=V_{M.PQE}-\left(V_{E.NQF}+V_{P.NQF}\right)\)
Có:
\(V_{M.PQE}=\dfrac{1}{3}AD.\dfrac{1}{2}DQ.PQ=\dfrac{1}{12}AD.D'D.CD=\dfrac{1}{12}V\)
\(V_{E.NQF}=\dfrac{1}{3}.ED.\dfrac{1}{2}ND.QF=\dfrac{1}{3}.\dfrac{1}{2}CD.\dfrac{1}{2}.\dfrac{1}{2}AD.\dfrac{1}{3}D'D=\dfrac{1}{72}V\)
\(V_{P.NQF}=\dfrac{1}{3}.PQ.\dfrac{1}{2}ND.QF=\dfrac{1}{3}CD.\dfrac{1}{2}.\dfrac{1}{2}AD.\dfrac{1}{3}D'D=\dfrac{1}{36}V\)
\(\Rightarrow V_{MNPQ}=\dfrac{1}{12}V-\left(\dfrac{1}{72}V+\dfrac{1}{36}V\right)=\dfrac{V}{24}\)
Bài này áp hệ trục tọa độ giải có lẽ sẽ ngắn hơn
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 12 2022
43.
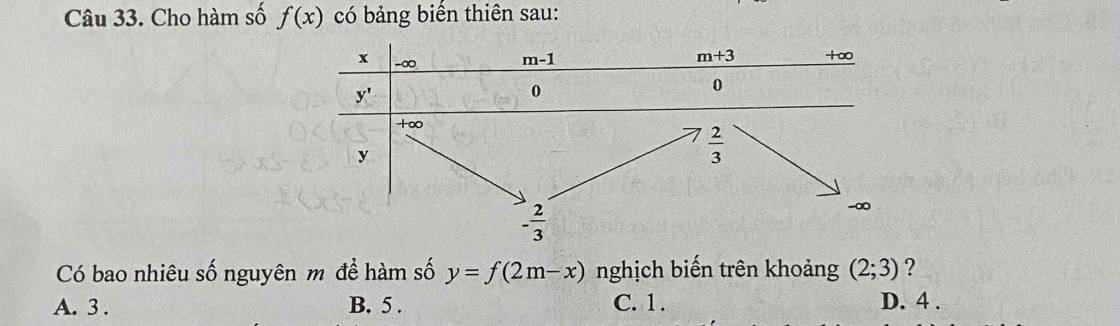
\(y'=2f'\left(2x+m\right)\) có cùng tính đơn điệu với hàm \(f\left(x\right)\)
Mà \(f\left(x\right)\) đồng biến trên \(\left(-1;1\right)\) và \(\left(4;+\infty\right)\)
\(\Rightarrow y=f\left(2x+m\right)\) đồng biến trên các khoảng thỏa mãn:
\(\left[{}\begin{matrix}-1\le2x+m\le1\\2x+m\ge4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\dfrac{-1-m}{2}\le x\le\dfrac{1-m}{2}\\x\ge\dfrac{4-m}{2}\end{matrix}\right.\)
Hàm đồng biến trên \(\left(1;2\right)\) khi và chỉ khi:
\(\left[{}\begin{matrix}\dfrac{-1-m}{2}\le1< 2\le\dfrac{1-m}{2}\\1\ge\dfrac{4-m}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-3\\m\ge2\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2022
\(\int\limits^4_3\dfrac{dx}{x^2+x}=\int\limits^4_3\dfrac{dx}{x\left(x+1\right)}=\int\limits^4_3\left(\dfrac{1}{x}-\dfrac{1}{x+1}\right)dx=\left[lnx-ln\left(x+1\right)\right]|^4_3\)
\(=ln4-ln5-\left(ln3-ln4\right)=2ln4-ln3-ln5\)
\(=4ln2-ln3-ln5\Rightarrow a=4;b=c=-1\)
\(\Rightarrow S=2\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 6 2021
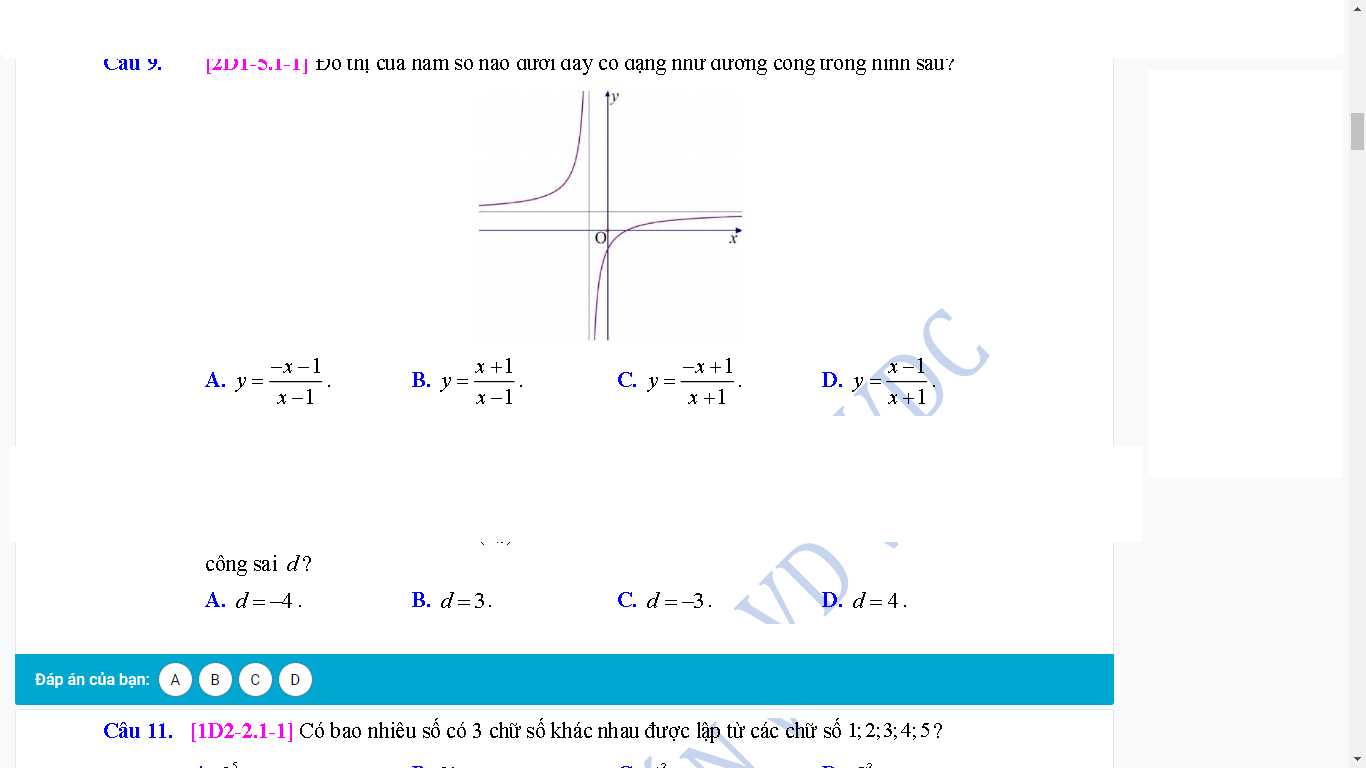
- Tiệm cận đứng của đồ thị là 1 giá trị âm nên loại A và B
- Hàm đồng biến trên các khoảng xác định nên loại C
Vậy D là đáp án đúng
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
Xét \(I_1=\int\limits^{\dfrac{\pi}{3}}_{\dfrac{\pi}{4}}\dfrac{f\left(tanx\right)}{cos^2x}dx=\int\limits^{\dfrac{\pi}{3}}_{\dfrac{\pi}{4}}f\left(tanx\right)d\left(tanx\right)\)
Đặt \(tanx=t\Rightarrow t\in\left[1;\sqrt{3}\right]\Rightarrow f\left(t\right)=2t^3-t\)
\(I_1=\int\limits^{\sqrt{3}}_1f\left(t\right)dt=\int\limits^{\sqrt{3}}_1\left(2t^3-t\right)dt=3\)
Xét \(I_2=\int\limits^{\sqrt{e-1}}_0\dfrac{xf\left(ln\left(x^2+1\right)\right)}{x^2+1}dx=\dfrac{1}{2}\int\limits^{\sqrt{e-1}}_0f\left(ln\left(x^2+1\right)\right).d\left[ln\left(x^2+1\right)\right]\)
Đặt \(ln\left(x^2+1\right)=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=-3t+4\)
\(I_2=\dfrac{1}{2}\int\limits^1_0\left(-3t+4\right)dt=\dfrac{5}{4}\)
\(\Rightarrow I=3+\dfrac{5}{4}=\dfrac{17}{4}\Rightarrow P=21\)