
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


|x - 5| - |2x - 4| = 0
<=> |x - 5| = 0 + |2x - 4|
<=> |x - 5| = |2x - 4|
Xét 2 trường hợp: 2x - 4 = x - 5
2x - 4 = -(x - 5)
TH1: 2x - 4 = x - 5
<=> 2x - 4 - x = -5
<=> x - 4 = -5
<=> x = -5 + 4
<=> x = -1
TH2: 2x - 4 = -(x - 5)
<=> 2x - 4 = -x + 5
<=> 2x - 4 + x = 5
<=> 3x - 4 = 5
<=> 3x = 5 + 4
<=> 3x = 9
<=> x = 3
=> x = 3
Vậy: x = -1 hoặc x = 3

a^2+b^2/ 9+16=102/25
=>a^2=109/25.9=981/25=>a=căn 981/25
=>b^2=109/25.16=1744/25=>b= căn 1744/25
a2/9 = b2/6 = (a2+b2)/(9+6) = 102/15 = 6,8 (tính chất dãy tỉ số bằng nhau)
=> a2 = 6,8.9 = 61,2 = > a = \(\sqrt{61,2}\)
b2 = 6,8.16 = 108,8 => b = \(\sqrt{108,8}\)

Lời giải:
Ta thấy, với mọi $x,y,z$ thì:
$(x-5)^2\geq 0$
$|2x-y|\geq 0$
$|x-2y+z|\geq 0$
$\Rightarrow A\geq 0+0+0-1=-1$
Vậy $A_{\min}=-1$.
Giá trị này đạt được khi $x-5=2x-y=x-2y+z=0$
$\Leftrightarrow x=5; y=10; z=15$

\(...=-\dfrac{4}{7}-\dfrac{3}{11}+\dfrac{3}{11}-\dfrac{3}{7}=-\dfrac{4}{7}-\dfrac{3}{7}=-1\)
-(4/7 + 3/11) - (-3/11 + 3/7)
= (-4/7) + (-3/11) - (-3/11) - 3/7
= [(-4/7) - 3/7)] + [(-3/11) - (-3/11)]
= -1 + 0
= -1

Câu 2:
\(1.f\left(x\right)=2x^3+x^2-3x+9.\\ g\left(x\right)=-2x^3-x^2+3.\)
Câu 3:
1. Ta có: \(AB=AC\) (\(\Delta ABC\) cân).
Mà \(AC=IC\left(gt\right). \)
\(\Rightarrow AB=IC.\)
Ta có: \(\widehat{ABC}=\widehat{ACB}\) (\(\Delta ABC\) cân).
Mà \(\widehat{ACB}=\widehat{ICE}\) (đối đỉnh).
\(\Rightarrow\widehat{ABC}=\widehat{ICE}.\)
Hay \(\widehat{ABD}=\widehat{ICE}.\)
Xét \(\Delta ABD\) và \(\Delta ICE:\)
BD = CE (gt).
\(\widehat{ABD}=\widehat{ICE}\left(cmt\right).\)
AB = IC (cmt).
\(\Rightarrow\Delta ABD=\Delta ICE\left(c-g-c\right).\)
2. Xét \(\Delta BDM\) và \(\Delta CEN:\)
\(\widehat{MBD}=\widehat{NCE}\left(\widehat{ABD}=\widehat{ICE}\right).\)
\(BD=CE\left(gt\right).\)
\(\widehat{BDM}=\widehat{CEN}\left(=90^o\right).\)
\(\Rightarrow\Delta BDM=\Delta CEN\left(g-c-g\right).\)
\(\Rightarrow BM=CN\) (2 cạnh tương ứng).

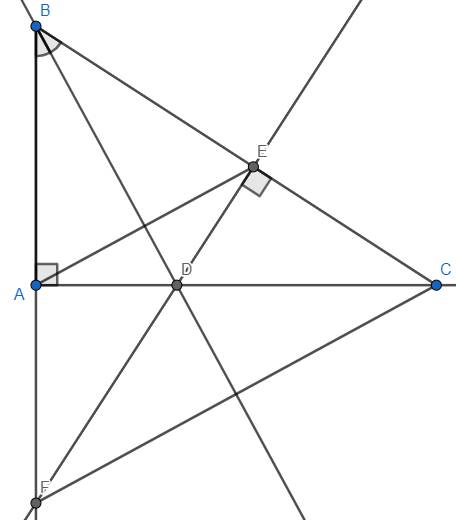
c) Ta đã biết DA = DE (chứng minh trên) (1)
Trong tam giác EDC vuông tại E có DC đối diện đỉnh E
Suy ra DC là cạnh lớn nhất trong tam giác EDC
Hay DC > DE (2)
Từ (1) và (2) suy ra DC > AD hay AD < DC

d: Xét ΔABK và ΔCKB có
AB=CK
KB chung
AK=CB
Do đó: ΔABK=ΔCKB

ta có D= -x^2-x-1 mà -x^2 <0 =>-x^2-x-1 < 0
cm tương tự ta có E,F < 0 với mọi giá trị của x

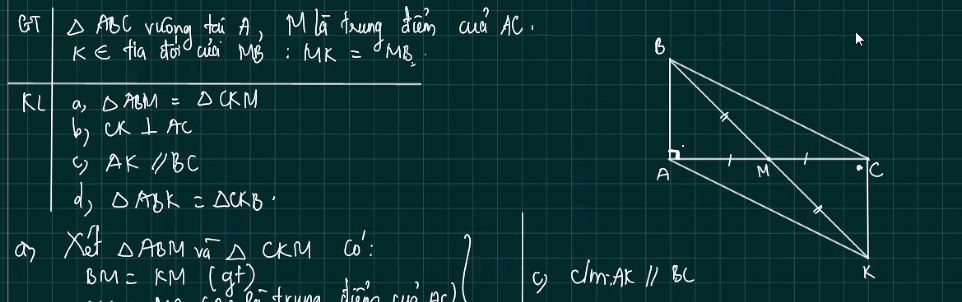 giúp mình câu d với
giúp mình câu d với