K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 9 2023
\(sđ\left(Ox;Ou\right)=-260^o=-260^o+360^o=100^0\)
mà \(sđ\left(Ox;Ov\right)=150^o\)
\(\Rightarrow sđ\left(Ou;Ov\right)=150^o-100^0=50^0\)
PT
1
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
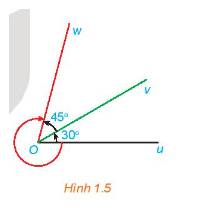
a) Ta có:
- Các góc lượng giác tia đầu Ou, tia cuối Ov có số đo là
sđ\((Ou,Ov) = {30^ \circ } + n{.360^ \circ }\)
- Các góc lượng giác tia đầu Ov, tia cuối Ow có số đo là
sđ \((Ov,Ow) = {45^ \circ } + m{.360^ \circ }\)
- Các góc lượng giác tia đầu Ou, tia cuối Ow có số đo là
sđ \((Ou,Ow) = {75^ \circ } + k{.360^ \circ }\)
b) Với các góc lượng giác ở câu a, ta có:
\(sđ(Ou,Ov) +sđ (Ov,Ow)\)
\( = {30^ \circ } + n{.360^ \circ } + {45^ \circ } + m{.360^ \circ } \)
\(= {75^ \circ } + (n+m){.360^ \circ } \)
\(= {75^ \circ } + k{.360^ \circ = sđ (Ou,Ow)} \)
với k = n + m
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Theo hệ thức Chasles, ta có:
\(\begin{array}{l}(Ov,Ow) = (Ou,Ov) - (Ou,Ow) + k2\pi \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \, - \frac{{11\pi }}{4} - \frac{{3\pi }}{4} + k2\pi = - \frac{7}{2} + k2\pi ,\,\,(k \in \mathbb{Z})\end{array}\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta có:
\((O'u',O'v') = (Ou,Ov) + k2\pi \,\, = \, - \frac{{4\pi }}{3}\, + k2\pi \,\,\,\,\,\,\,\,(k \in \mathbb{Z})\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
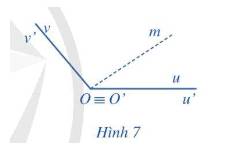
Quan sát Hình 7 ta thấy:
• Tia Om quay (chỉ theo chiều dương) xuất phát từ tia Ou đến trùng với tia Ov rồi quay tiếp một số vòng đến trùng với tia cuối Ov;
• Tia Om quay (chỉ theo chiều dương) xuất phát từ tia \(O'u' \equiv Ou\) đến trùng với tia \(O'v' \equiv Ov\)rồi quay tiếp một số vòng đến trùng với tỉa cuối \(O'v' \equiv Ov\).
Như vậy, sự khác biệt giữa hai góc lượng giác (Ou, Ov) và (O’u’, O’v’) chính là số vòng quay quanh điểm O. Vì vậy, sự khác biệt giữa số đo của hai góc lượng giác đó chính là bội nguyên của \({360^ \circ }\) khi hai góc đó tính theo đơn vị độ (hay bội nguyên của \(2\pi \) rad khi hai góc đó tính theo đơn vị radian).
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Ta có:
- Các góc lượng giác tia đầu Ou, tia cuối Ov có số đo là \((Ou,Ov) = {45^ \circ } + k{.360^ \circ }\)
b) Ta có:
- Các góc lượng giác tia đầu Ou, tia cuối Ov có số đo là \((Ou,Ov) = - {315^ \circ } + k{.360^ \circ }\)
21 tháng 9 2023
Tham khảo:
Ta có \( - \frac{{5\pi }}{4} = - \pi + \left( { - \frac{\pi }{4}} \right)\). Góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo \( - \frac{{5\pi }}{4}\) được biểu diễn ở hình sau:
PT
1
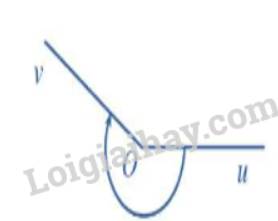
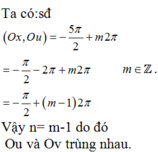
\(sđ\left(Ou;Ov\right)=sđ\left(Ox;Ov\right)-sđ\left(Ox;Ou\right)\)
\(=150^0-\left(-260^0\right)+k\cdot360^0\)
\(=410^0+k\cdot360^0\)
\(=50^0+\left(k-1\right)\cdot360^0\)