K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

13 tháng 1 2023
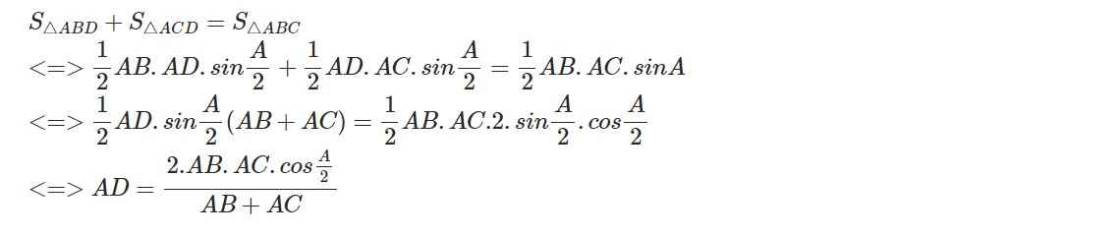
=>\(\dfrac{1}{AB}+\dfrac{1}{AC}=\dfrac{\sqrt{2}}{AD}\)

P
17 tháng 2 2018
t ghi nhầm cái dòng thứ 2 từ dưới lên la ME voi HE đều vuong goc voi AB
Chứng minh vế phải này ; phương pháp đại số nha
\(S_{ABC}=\frac{AB.AC}{2}=1\Rightarrow AB.AC=2\)
Theo pytago Tam giác ABC vuông tại A \(\Rightarrow AB^2+AC^2=BC^2\)
BĐT cần cm : \(BC\le\sqrt{2}\left(AB+AC-\sqrt{2}\right)\)
\(\Leftrightarrow BC\le\sqrt{2}\left(AB+AC\right)-2\)
\(\Leftrightarrow\left(BC+2\right)^2\le2\left(AB+AC\right)^2\)
\(\Leftrightarrow BC^2+4BC+4\le2AB^2+2AC^2+4AB.AC\)
\(\Leftrightarrow AB^2+AC^2+4BC+4\le2AB^2+2AC^2+4.2\)( \(AB^2+AC^2=BC^2\)Và\(AB.AC=2\))
\(\Leftrightarrow4BC\le AB^2+AC^2+4\)
\(\Leftrightarrow4BC\le BC^2+4\)
\(\Leftrightarrow-BC^2+4BC-4\le0\)
\(\Leftrightarrow-\left(BC-2\right)^2\le0\)(Luôn đúng)
Vậy bđt đã được chứng minh
vì tam giác ABC vuông tại A =>\(BC^2=AB^2+AC^2\ge2AB.AC=4\) (vì \(S_{ABC}=\frac{AB.AC}{2}\Rightarrow AB.AC=2\) )
\(\Rightarrow BC\ge2\) (ĐPCM)
dấu = xảy ra <=> tam giác ABC vuông cân tại A
^_^