Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f\left(-x\right)=-x^3+\left(m^2-1\right)x^2-2x+m-1\)
Để hàm là hàm lẻ thì \(f\left(x\right)+f\left(-x\right)=0\) \(\forall x\)
\(\Leftrightarrow2\left(m^2-1\right)x^2+2m-2=0\) \(\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(m^2-1\right)=0\\2m-2=0\end{matrix}\right.\) \(\Rightarrow m=1\)


Coi lại đề, cái ngoặc thứ 2 ấy, \(m^2-3x+2\) là có vấn đề rồi

a: \(f\left(-2\right)=\left(-2\right)^2+3\cdot\left(-2\right)-1\)
=4-6-1
=-3
\(f\left(-1\right)=\left(-1\right)^2+3\cdot\left(-1\right)-1\)
\(=1-3-1\)
=-3

Lời giải:
Với $m=m_0$ thì:
\(f(x)=x^3+(m_0^2-1)x^2+2x+m_0-1\)
Vì hàm $f(x)$ là hàm lẻ nên: \(f(-x)=-f(x)\) với mọi \(x;-x\in \) TXĐ
\(\Leftrightarrow (-x)^3+(m_0^2-1)(-x)^2+2(-x)+m_0-1=-[x^3+(m_0^2-1)x^2+2x+m-1]\)
\(\Leftrightarrow (m_0^2-1)x^2+m_0-1=-(m_0^2-1)x^2-(m_0-1)\)
\(\Leftrightarrow (m_0^2-1)x_0^2+m_0-1=0\)
\(\Leftrightarrow (m_0-1)[(m_0+1)x_0^2+1]=0\)
Vì điều trên đúng với mọi $x;-x\in$ TXĐ nên \(m_0-1=0\Rightarrow m_0=1\)
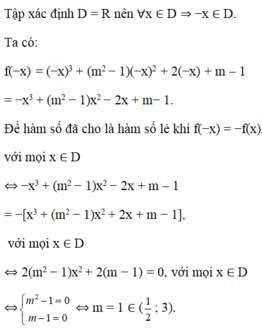

Để đây là hàm số lẻ thì f(-x)=-f(x)
\(\Leftrightarrow\left(-x\right)^3+\left(m^2-1\right)x^2+2\cdot\left(-x\right)+m-1=-x^3-\left(m^2-1\right)x^2-2x-m+1\)
=>2x^2(m^2-1)+2m-2=0
=>m=1