K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 11 2023
\(5^x+5^{x+1}+5^{x+2}+5^{x+3}=1+2+3+...+87+88-4^2\)
=>\(5^x+5^x\cdot5+5^x\cdot25+5^x\cdot125=88\cdot\dfrac{\left(88+1\right)}{2}-16\)
=>\(156\cdot5^x=44\cdot89-16=3900\)
=>\(5^x=\dfrac{3900}{156}=25\)
=>x=2
DT
1
AH
Akai Haruma
Giáo viên
2 tháng 12 2023
Lời giải:
$5^x+5^{x+1}+5^{x+2}+5^{x+3}=1+2+3+...+87+88-4^2$
$5^x(1+5+5^2+5^3)=88.89:2-16$
$5^x.156=3900$
$5^x=3900:156=25=5^2$
$\Rightarrow x=2$
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
24 tháng 1
5x+5x+1+5x+2=31
5x + 5x + 5x = 31 - 2 - 1
15x = 28
x= 28/15
24 tháng 9 2016
a, 42x - 6 = 1
=> 42 x = 7
=> x = 6
b, 5x + 5x + 1 +5x + 2 = 775
=> 15 x + 3 = 775
=> 15 x = 772
=> x = 772/ 15
KV
30 tháng 8 2023
2⁵ˣ⁺¹ - 2⁵ˣ = 32
2⁵ˣ.(2 - 1) = 2⁵
2⁵ˣ = 2⁵
5x = 5
x = 5 : 5
x = 1
H9
HT.Phong (9A5)
CTVHS
30 tháng 8 2023
\(2^{5x+1}-2^{5x}=32\)
\(\Rightarrow2^{5x+1}-2^{5x}=2^5\)
\(\Rightarrow2^{5x}\cdot2-2^{5x}\cdot1=2^5\)
\(\Rightarrow2^{5x}\cdot\left(2-1\right)=2^5\)
\(\Rightarrow2^{5x}\cdot1=2^5\)
\(\Rightarrow2^{5x}=2^5\)
\(\Rightarrow5x=5\)
\(\Rightarrow x=\dfrac{5}{5}\)
\(\Rightarrow x=1\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
6 tháng 9 2023
3\(x^2\).(5\(x\) + 1) + 6\(x^3\).(5\(x\) + 2) = 9\(x^3\) .(5\(x\) + 3)
15\(x^3\) + 3\(x^2\) + 30\(x^4\) + 12\(x^3\) = 45\(x^4\) + 27\(x^3\)
(15\(x^3\) + 12\(x^3\)) + 3\(x^2\) + 30\(x^4\) - 45\(x^4\) - 27\(x^3\) = 0
27\(x^3\) + 3\(x^2\) - 15\(x^4\) - 27\(x^3\) = 0
3\(x^2\) - 15\(x^4\) = 0
3\(x^2\).(1 - 5\(x^2\)) = 0
\(\left[{}\begin{matrix}x^2=0\\1-5x^2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\5x^2=1\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=\mp\dfrac{\sqrt{5}}{5}\end{matrix}\right.\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 10 2023
5\(^{x+1}\) - 5\(^x\) = 2.28 + 8
5\(^x\).(5 - 1) = 520
5\(^x\).4 = 520
5\(^x\) = 520 : 4
5\(^x\) = 130
Với \(x\) = 0 ⇒ 5\(^x\) = 50 = 1 < 130 (loại)
Với \(x\) > 0 ⇒ 5\(^x\) = \(\overline{...5}\) \(\ne\) 130 (loại)
Vậy \(x\) \(\in\) \(\varnothing\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
16 tháng 10 2023
\(5^{x+1}-5^x=2.2^8+8\\ 5^x\left(5-1\right)=512+8\\ 5^x.4=520\\ 5^x=\dfrac{520}{4}=130\)
Em xem lại đề
18 tháng 9 2021
\(5^x+5^{x+2}+5^{x+4}=3255\)
\(\Rightarrow5^x\left(1+5^2+5^4\right)=3255\)
\(\Rightarrow5^x.651=3255\)
\(\Rightarrow5^x=5\Rightarrow x=1\)
9 tháng 8 2021
Bạn thử xem lại đề nhé, giữa 3 số này là dấu cộng hay dấu nhân.
Nếu là dấu cộng thì ta có:
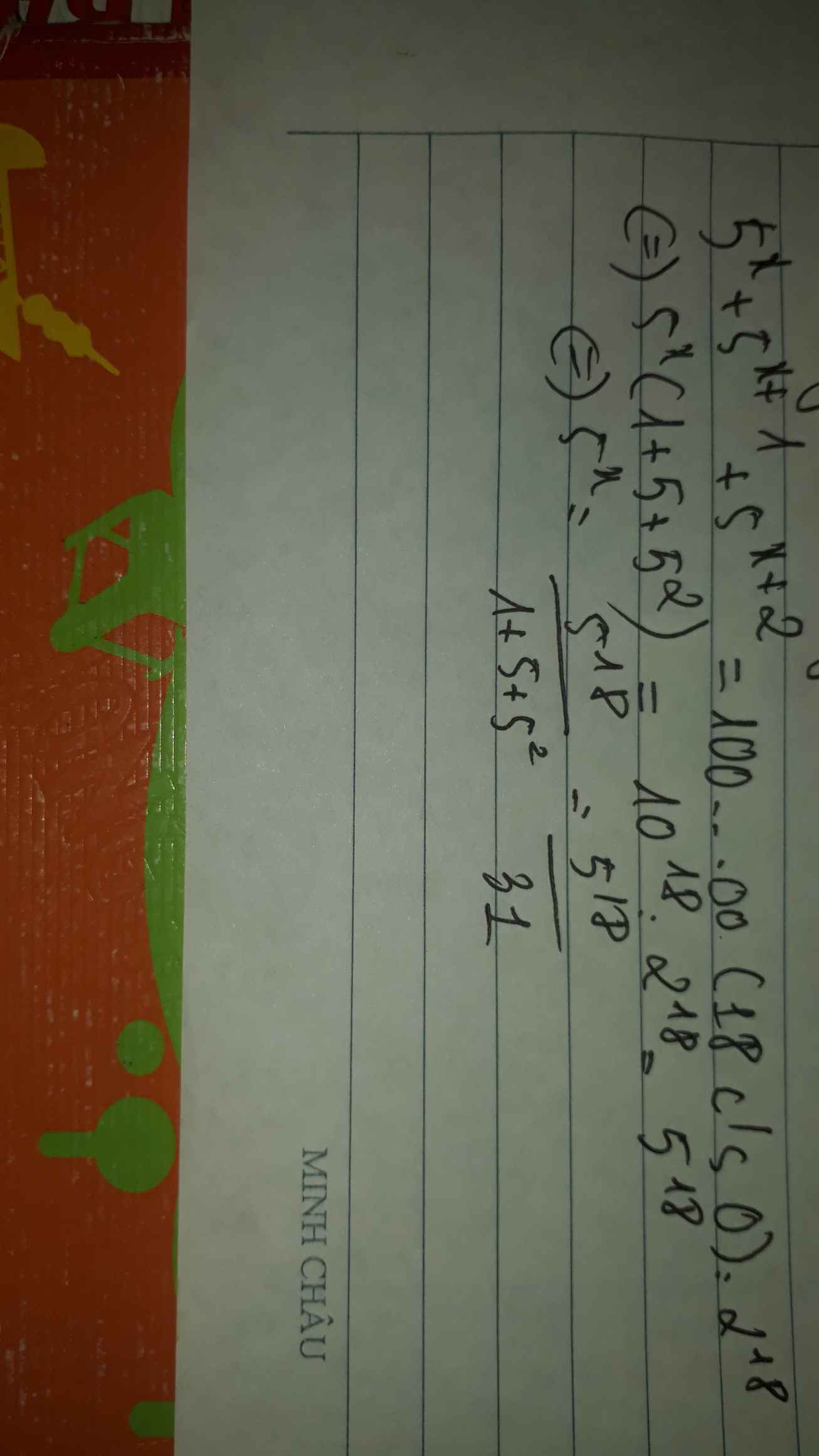
Nếu là dấu nhân thì ta có:
BB
6
5 tháng 5 2019
\(\frac{5x+4}{2006}+\frac{5x+3}{2007}=\frac{5x+2}{2008}+\frac{5x+1}{2009}\)
\(\Leftrightarrow\frac{5x+4}{2006}+1+\frac{5x+3}{2007}+1=\frac{5x+2}{2008}+1+\frac{5x+1}{2009}+1\)
\(\Leftrightarrow\frac{5x+2010}{2006}+\frac{5x+2010}{2007}=\frac{5x+2010}{2008}+\frac{5x+2010}{2009}\)
\(\Leftrightarrow\left(5x+2010\right)\left(\frac{1}{2006}+\frac{1}{2007}\right)=\left(5x+2010\right)\left(\frac{1}{2008}+\frac{1}{2009}\right)\)
\(\Leftrightarrow5x+2010=0\)
\(\Leftrightarrow5x=-2010\)
\(\Leftrightarrow x=-402\)
\(5^x+5^{x+1}+5^{x+2}=31.5^6\)
\(\Rightarrow\)\(5^x.\left(1+5^1+5^2\right)=31.5^6\)
\(\Rightarrow\)\(5^x.31=31.5^6\)
\(\Rightarrow\)\(5^x=5^6\)
\(\Rightarrow\)\(x=6\)