lm giúpppp e gấppppp vsss
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 9 2023
3:
ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*CB
=>BH/CH=(AB/AC)^2=9/16
=>BH/9=CH/16
=>\(\dfrac{BH}{9}=\dfrac{CH}{16}=\dfrac{BH+CH}{9+16}=\dfrac{15}{25}=0.6\)
=>BH=5,4cm; CH=9,6cm
2:
a: ΔABC vuông tại A
=>BC^2=AB^2+AC^2
=>BC=căn 3^2+4^2=5(cm)
ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC; AB^2=BH*BC; AC^2=CH*CB
=>AH=3*4/5=2,4cm; BH=3^2/5=1,8cm; CH=4^2/5=3,2cm
b:
BC=BH+CH=25cm
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC; AB^2=BH*BC; AC^2=CH*CB
=>AH=căn 9*16=12cm; AB=căn 9*25=15cm; AC=căn 16*25=20cm
7 tháng 11 2021
\(=\left(\dfrac{7}{4}.\dfrac{2}{7}\right).\dfrac{4}{5}=\dfrac{1}{2}.\dfrac{4}{5}=\dfrac{2}{5}\)
7 tháng 11 2021
a/\(\left(1,75:\dfrac{7}{2}\right).\dfrac{4}{5}=\left(\dfrac{7}{4}:\dfrac{7}{2}\right).\dfrac{4}{5}=\dfrac{1}{2}.\dfrac{4}{5}\dfrac{2}{5}\)
3 tháng 12 2021
Cách 2:
if (b%2==0) cout<<"b la so chan";
else cout<<"b la so le";
26 tháng 2 2022
a: \(=\left(2+\dfrac{4}{9}+4+\dfrac{5}{9}\right)+\left(-4-\dfrac{13}{21}-2-\dfrac{8}{21}\right)\)
=7-7
=0
b: \(=\dfrac{5}{23}\left(\dfrac{7}{13}+\dfrac{6}{13}\right)+\dfrac{18}{23}=\dfrac{5}{23}+\dfrac{18}{23}=1\)
c: \(=\dfrac{3}{7}\left(\dfrac{12}{19}-\dfrac{4}{19}\right)+\dfrac{4}{7}\cdot\dfrac{8}{19}\)
\(=\dfrac{3}{7}\cdot\dfrac{8}{19}+\dfrac{4}{7}\cdot\dfrac{8}{19}=\dfrac{8}{19}\)
d: \(=\dfrac{2}{5}+\dfrac{3}{5}:\dfrac{9-10}{15}-\dfrac{7}{2}\)
\(=\dfrac{-31}{10}+\dfrac{3}{5}\cdot\dfrac{-15}{1}=\dfrac{-31}{10}-9=\dfrac{-121}{10}\)
28 tháng 2 2022
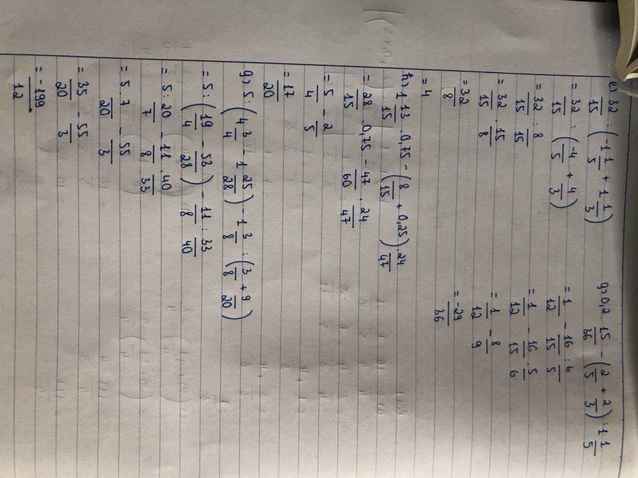
a: \(=\dfrac{48}{36}+\dfrac{7}{5}\cdot\dfrac{20}{21}=\dfrac{4}{3}+\dfrac{4}{3}=\dfrac{8}{3}\)
b: \(=\dfrac{7}{3}-\dfrac{1}{3}\cdot\left[-\dfrac{3}{2}+\dfrac{2}{3}+\dfrac{4}{10}\cdot5\right]\)
\(=\dfrac{7}{3}-\dfrac{1}{3}\cdot\dfrac{7}{6}=\dfrac{7}{3}-\dfrac{7}{18}=\dfrac{42-7}{18}=\dfrac{35}{18}\)
c: \(=\left(29+\dfrac{1}{4}\right):\dfrac{9}{4}=\dfrac{117}{4}\cdot\dfrac{4}{9}=\dfrac{117}{9}=13\)
d: \(=\left(4-\dfrac{4}{5}\right)\cdot\dfrac{11}{8}-\dfrac{8}{5}\cdot4\)
\(=\dfrac{16}{5}\cdot\dfrac{11}{8}-\dfrac{32}{5}\)
\(=\dfrac{22}{5}-\dfrac{32}{5}=-\dfrac{10}{5}=-2\)
PM
1
DT
Đỗ Thanh Hải
CTVVIP
2 tháng 7 2021
1 He lives with his family in a small town near HN
2 They are workers
3 They go there by motorbike
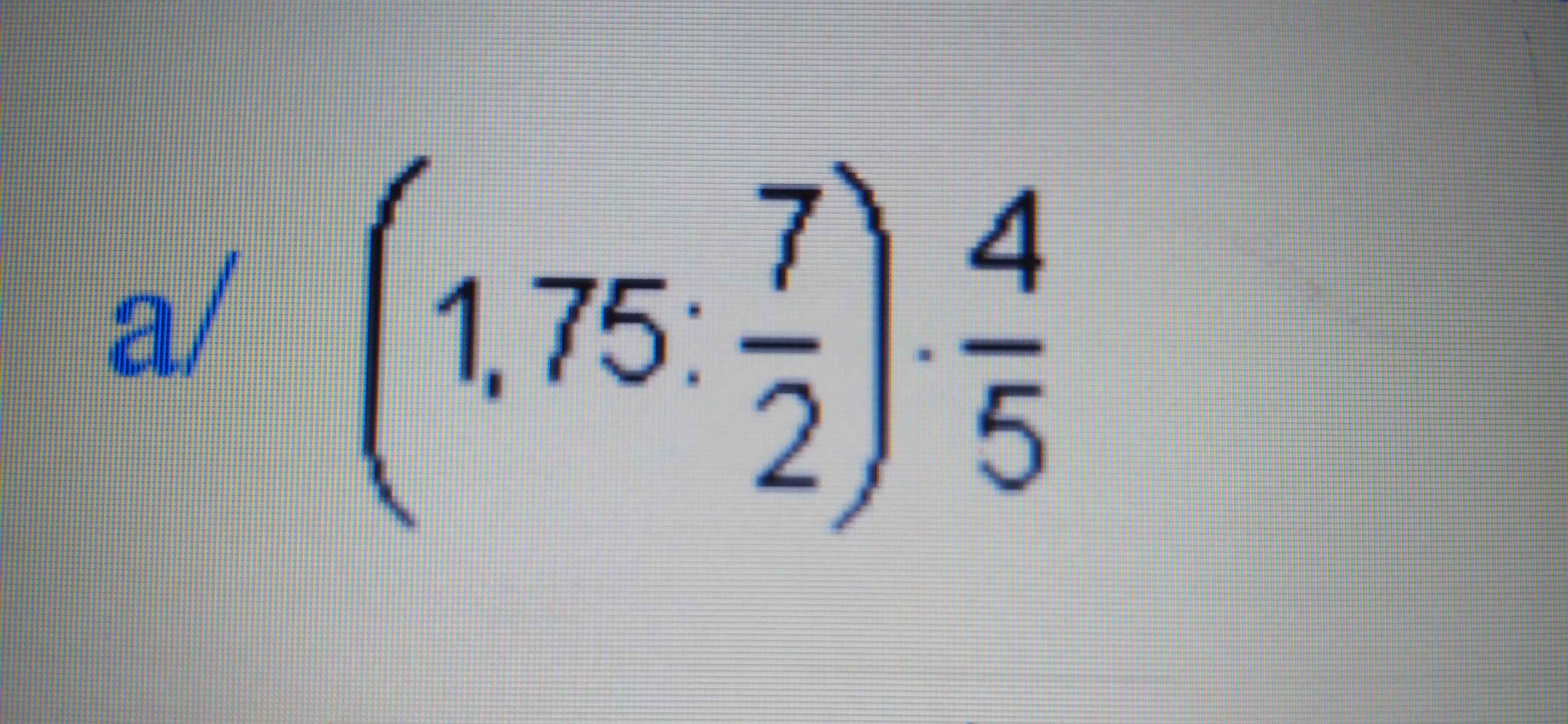
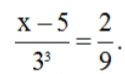
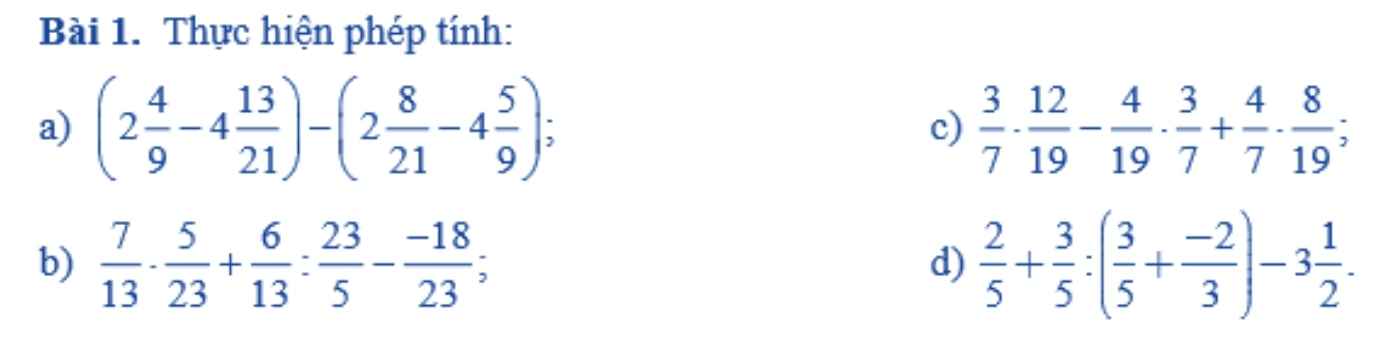
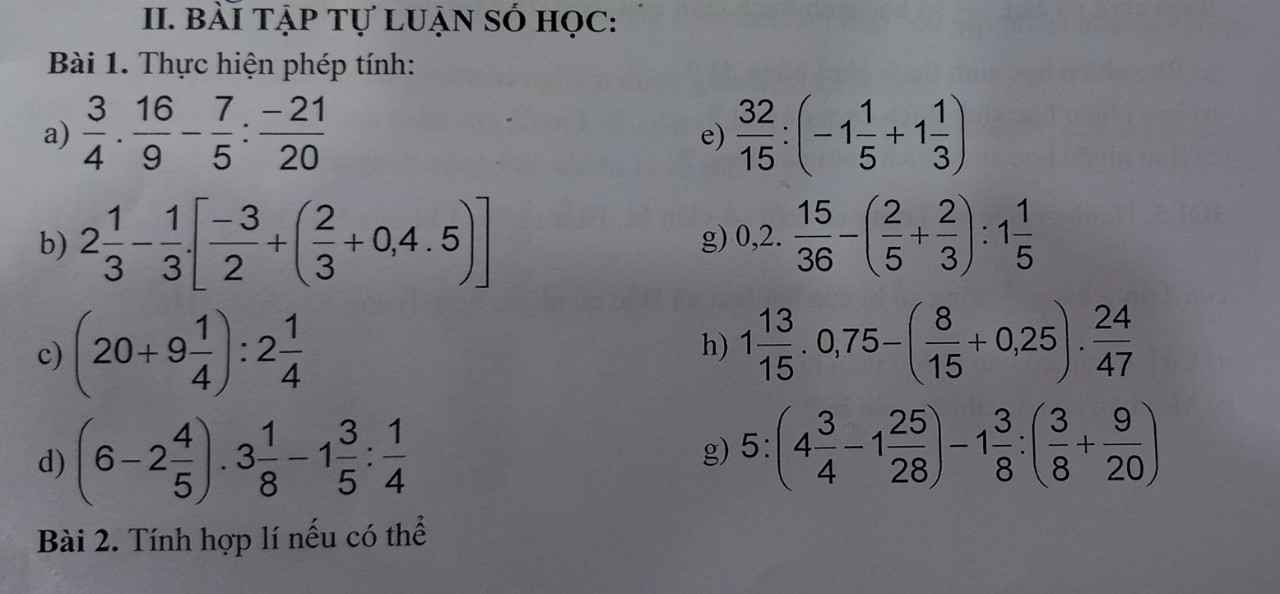
d: \(3x^2+x-6-\sqrt{2}=0\)
\(\Delta=1^2-4\cdot3\cdot\left(-6-\sqrt{2}\right)\)
\(=1+72+12\sqrt{2}=73+12\sqrt{2}\)
\(=\left(6\sqrt{2}+1\right)^2>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{\left(-1-\left(6\sqrt{2}+1\right)\right)}{2\cdot3}=\dfrac{-1-6\sqrt{2}-1}{6}=\dfrac{-2-6\sqrt{2}}{6}=\dfrac{-3\sqrt{2}-1}{3}\\x=\dfrac{-1+\left(6\sqrt{2}+1\right)}{6}=\dfrac{6\sqrt{2}}{6}=\sqrt{2}\end{matrix}\right.\)
e: ĐKXĐ: x<>-1
\(\dfrac{2}{x^2-x+1}=\dfrac{1}{x+1}+\dfrac{2x-1}{x^3+1}\)
=>\(\dfrac{2}{x^2-x+1}=\dfrac{1}{x+1}+\dfrac{2x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
=>\(\dfrac{2\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x^2-x+1+2x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
=>\(x^2+x=2x+2\)
=>(x+1)(x-2)=0
=>\(\left[{}\begin{matrix}x=-1\left(loại\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
( 3x2 -6) + (x-v2) = 0
3(x2-2) +(x-v2)=0
3(x-v2)(x+v2) +(x-v2)=0
đặt (x-v2) làm TSC.