Đố ai biết tứ giác nội tiếp là gì ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tứ giác nội tiếp là tứ giác có 4 đỉnh nằm trên một đường tròn.

Gọi đường tròn (BIC) cắt BD trại G khác B. Trên đoạn AD lấy E' sao cho AE' = AF.
Xét \(\Delta\)AIF và \(\Delta\)AIE': AF = AE', ^IAF = ^IAE', AI chung => \(\Delta\)AIF = \(\Delta\)AIE' (c.g.c) => IF = IE'
Xét (BIC): ^FBG nội tiếp, BI là phân giác ^FBG, I thuộc (BIC) => (IF = (IG => IF = IG. Từ đó IG = IE'
Dễ thấy: ^IE'A = ^IFA (Do \(\Delta\)AIF = \(\Delta\)AIE') => ^IFB = ^IE'D hay ^IE'D = ^IGD
Từ đó: ^GID = ^E'ID (Vì ^IDE' = ^IDG), kết hợp với IG = IE', cạnh ID chung => \(\Delta\)DGI = \(\Delta\)DE'I (c.g.c)
Suy ra: DG = DE'. Ta lại có: ^CAB = ^CDB; ^CFB = ^CGB => ^FCA = ^GCD
Xét \(\Delta\)CFA và \(\Delta\)CGD: CA = CD; ^CAF = ^CDG; ^FCA = ^GCD => \(\Delta\)CFA = \(\Delta\)CGD (g.c.g)
=> AF = DG. Mà DG = DE' nên AF = DE'. Do đó: DE' = AE' => E' là trung điểm AD => E' trùng E
Như vậy AE = AF và IF = IE suy ra AI là trung trực của EF hay AI vuông góc EF (đpcm),
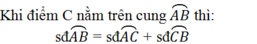
Tứ giác nội tiếp là tứ giác có 4 đỉnh nằm trên 1 đường tròn.
Một tứ giác nội tiếp có thể được chia nhỏ thành vô số các tứ giác nội tiếp khác.
Từ đa giác nội tiếp lớn ban đầu hãy sắp đặt đa giác sao cho cạnh kề với hai góc nhọn ở dưới. Sau đó kẻ ba đường thẳng song song với ba cạnh để tạo thành hai hình thang cân (1) và (2). Hình thang còn lại, (3), tuy không phải là cân nhưng là tứ giác nội tiếp. Hình (4) có các cạnh song song với tứ giác nội tiếp ban đầu nên đồng dạng và do đó cũng là tứ giác nội tiếp.
Ta có thể áp dụng cách như trên đối với hình (4) để được (vô số) các tứ giác nội tiếp; cũng như phân chia các hình thang cân (1) và (2) thành vô số các hình thang cân (nội tiếp) khác.
Nếu gọi a,b,c,d là độ dài 4 cạnh của tứ giác. p và q là độ dài của hai đường chéo. S là diện tích của tứ giác. R là bán kính đường tròn ngoại tiếp tứ giác. Ta có các công thức:
{\displaystyle {\frac {p}{q}}={\frac {ad+cb}{ab+cd}},\quad p^{2}={\frac {(ac+bd)(ad+bc)}{ab+cd}}\quad {\text{và}}\quad q^{2}={\frac {(ac+bd)(ab+dc)}{ad+bc}}.}
{\displaystyle S={\frac {\sqrt {(ac+bd)(ad+bc)(ab+cd)}}{4R}}\,}