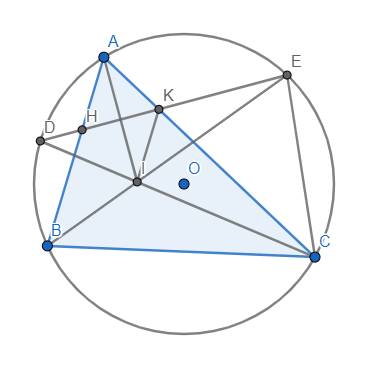
Cho tam giác nhọn ABC nội tiếp đường tròn (O), D và E theo thứ tự là điểm chính giữa của cung nhỏ AB,AC.Gọi giao điểm của DE với AB và AC lần lượt H và K.
a.chứng minh tam giác AHK cân
b.gọi I là giao điểm của CD và BE.Chứng minh AI vuông góc với DE
c.chứng minh IK song song với AB