Cho tam giác ABC cân tại A, có \(\widehat{A}\) = 200. Trên cạnh AC lấy điểm D sao cho AD = BC. Tìm \(\widehat{ADC}\)= ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trên nửa mặt phẳng bờ BC dựng \(\Delta\)BCE đều
Xét \(\Delta\)BAE và \(\Delta\) CAE có:
AB = AC (\(\Delta\)ABC cân)
AE: chung
EB = EC (\(\Delta\)BCE đều)
\(\Rightarrow\)\(\Delta\)BAE = \(\Delta\) CAE (c.c.c)
\(\Rightarrow\)BAE = CAE (2 cạnh tương ứng)
\(\Rightarrow\)AE là phân giác BAC
\(\Rightarrow\)BAE = CAE = BAC : 2 = 20o : 2 = 10o
Vì \(\Delta\) ABC cân ở A \(\Rightarrow\)BCA = (180o - BAC) : 2 = 80o
Ta có: \(\Delta\)BCE đều \(\Rightarrow\)ECB = 60o
Có: ACE + ECB = ACB
\(\Rightarrow\)ACE = ACB - ECB = 80o - 60o = 20o
\(\Rightarrow\)ACE = CAD
Xét \(\Delta\)DAC và \(\Delta\)ECA có:
AC: chung
ACE = CAD (cmt)
EC = AD (= BC)
\(\Rightarrow\)\(\Delta\)DAC = \(\Delta\)ECA (c.g.c)
\(\Rightarrow\)EAC = ECA = 10o (2 góc tương ứng)
Ta có: BDC = DAC + ECA = 20o + 10o =30o
Vậy BDC = 30o

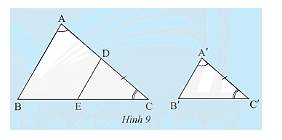
a) Vì \(ED//AB \Rightarrow \Delta DEC\backsim\Delta ABC\) (định lí)
b) Vì \(ED//AB \Rightarrow \widehat {CDE} = \widehat {CAB}\) (hai góc đồng vị)
Mà \(\widehat {CAB} = \widehat {A'}\). Do đó, \(\widehat {CDE} = \widehat {B'A'C'}\).
Xét tam giác \(A'B'C'\) và tam giác \(DEC\) ta có:
\(\widehat {B'A'C'} = \widehat {CDE}\) (chứng minh trên)
\(A'C' = CD\) (giải thuyết)
\(\widehat {C'} = \widehat C\) (giả thuyết)
Do đó, \(\Delta A'B'C' = \Delta DEC\) (g.c.g)
c) Vì tam giác \(\Delta A'B'C'\backsim\Delta DEC\) (tính chất)
Mà \(\Delta DEC\backsim\Delta ABC\) nên \(\Delta ABC\backsim\Delta A'B'C'\).

a) Xét \(\Delta\)BAE và \(\Delta\)DAC có: ^BAE = ^DAC ( đối đỉnh ) ; AD = AB ( gt ) ; AE = AC ( gt )
=> \(\Delta\)BAE = \(\Delta\)DAC ( c.g.c)
=> BE = DC
b) Tương tự câu a dễ dàng cm đc: \(\Delta\)ADE = \(\Delta\)ABC => ^ADE = ^ABC => DE//BC
=> ^EDI = ^DIC mà ^EDI = ^BDI ( DI là phân giác ^BDE )
=> ^DIC = ^BDI hay ^DIB = ^IDB => \(\Delta\)BDI cân tại B.
c) Ta có: ^DBC là góc ngoài tại đỉnh B của \(\Delta\)BDI => ^DBC = ^BDI + ^BID = 2. ^BID = 2. ^CIF( theo b) (1)
Có: CF là phân giác ^BCA =>^BCF = ^ACF => ^BCA = ^BCF + ^ACF = 2. ^BCF = 2. ^ICF (2)
Lại có: ^CFD là góc ngoài của \(\Delta\)FCI => ^CFD = ^CIF + ^ICF (3)
Từ (1) ; (2) ; (3) => 2 .^CFD = 2 ^CIF + 2. ^ICF = ^DBC + ^BCA = ^DBC + ^CED ( ^CED = ^BCA vì ED //BC )

b) Ta có: AD+DC=AC(D nằm giữa A và C)
nên DC=AC-AD=3-1=2(cm)
Ta có: DE=AD(gt)
mà AD=1cm(cmt)
nên DE=1cm
Ta có: \(\dfrac{BD}{CD}=\dfrac{\sqrt{2}}{2}\)
\(\dfrac{DE}{DB}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
Do đó: \(\dfrac{BD}{CD}=\dfrac{DE}{DB}\)\(\left(=\dfrac{\sqrt{2}}{2}\right)\)
Xét ΔBDE và ΔCDB có
\(\dfrac{BD}{CD}=\dfrac{DE}{DB}\)(cmt)
\(\widehat{BDE}\) chung
Do đó: ΔBDE\(\sim\)ΔCDB(c-g-c)
a) Ta có: AD+DE+EC=AC
mà AD=DE=EC(gt)
nên \(AD=\dfrac{AC}{3}=\dfrac{3}{3}=1\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow BD^2=1+1=2\)
hay \(BD=\sqrt{2}cm\)
Vậy: \(BD=\sqrt{2}cm\)

A) TRONG \(\Delta ABC\)TA VẼ \(\Delta EBC\)VUÔNG CÂN TẠI E;\(\widehat{EBC}=45^o\)
TA CÓ \(EB^2+EC^2=BC^2\)
\(2EB^2=4;EB^2=2;EB=\sqrt{2}\)
VẬY \(AD=EB=\sqrt{2}\)
\(\Delta BAE=\Delta CAE\left(C-G-C\right)\)
\(\Rightarrow\widehat{BAE}=\widehat{CAE}=15^o\)
\(\widehat{ABC}=\left(180^o-30^o\right):2=75^o;\widehat{ABE}=75^o-45^o=30^o;\)VẬY\(\widehat{ABE}=\widehat{BED}=30^o\)
\(\Delta ABD=\Delta BAE\left(C-G-C\right)\Rightarrow\widehat{ABE}=\widehat{BAE}=15^o\)
B)
\(\Delta DBC\)CÓ\(\widehat{DBC}=75^o-15^o=60^o;\widehat{DCB}=75^o\)VÀ\(\widehat{BDC}=45^o\)
\(\Rightarrow\widehat{BDC}< \widehat{DBC}< \widehat{DCB}\left(45^o< 60^o< 75^o\right)\)do đó BC<CD<BD( QUAN HỆ BA CẠNH VÀ GÓC ĐỐI DIỆN)
ᴾᴿᴼシĐệ❦℘ℛℴ༻꧂
-hình bạn vẽ thiếu dữ kiện nha
Tam giác ABC cân tại A , bạn phải kí hiệu AB=AC chứ