giải thích tại sao a(-c)(-b)=abc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
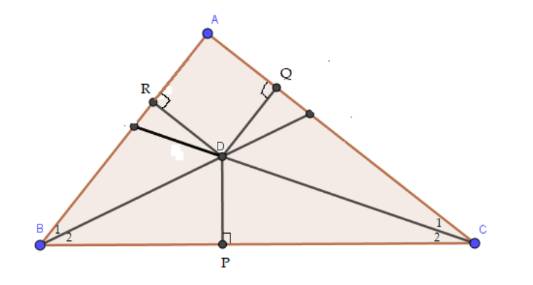
a) Vì BD là tia phân giác của góc ABC nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)
Vì CD là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)
Xét \(\Delta BDP\) vuông tại P và \(\Delta BDR\) vuông tại R, ta có:
\(\widehat {{B_2}} = \widehat {{B_1}}\)
BD chung
\( \Rightarrow \Delta BDP = \Delta BDR\) ( cạnh huyền – góc nhọn)
\( \Rightarrow \) DP = DR ( 2 cạnh tương ứng) (1)
b) Xét \(\Delta CDP\) vuông tại P và \(\Delta CDQ\) vuông tại Q, ta có:
\(\widehat {{C_2}} = \widehat {{C_1}}\)
CD chung
\( \Rightarrow \Delta CDP = \Delta CDQ\) ( cạnh huyền – góc nhọn)
\( \Rightarrow \) DP = DQ ( 2 cạnh tương ứng) (2)
c) Từ (1) và (2), ta được: DR = DQ ( cùng bằng DP).
D nằm trên tia phân giác của góc A do D cách đều AB và AC.
12 tháng 5 2022
\(a,\dfrac{a}{b}=\dfrac{ad}{bd}\) và \(\dfrac{c}{d}=\dfrac{bc}{bd}\). Do \(\dfrac{a}{b}< \dfrac{c}{d}\) nên \(\dfrac{ad}{bd}< \dfrac{bc}{bd}\).
Suy ra \(ad< bc\)
\(b,\dfrac{a}{b}< \dfrac{c}{d}\) suy ra \(ad< bc\). Do đó \(ab+ad< ab+bc\) nên \(a\left(b+d\right)< b\left(a+c\right)\)
Vậy \(\dfrac{a}{b}< \dfrac{a+c}{b+d}.\) Từ \(ad< bc\) ta cũng có \(ad+cd< bc+cd\) nên \(\left(a+c\right)d< \left(b+d\right)c\)
\(\Rightarrow\dfrac{a+c}{b+d}< \dfrac{c}{d}\)
17 tháng 5 2022
\(\dfrac{a}{b}=\dfrac{a\left(b+c\right)}{b\left(b+c\right)}=\dfrac{ab}{b\left(b+c\right)}+\dfrac{ac}{b\left(b+c\right)};\dfrac{a+c}{b+c}=\dfrac{b\left(a+c\right)}{b\left(b+c\right)}=\dfrac{ab}{b\left(b+c\right)}+\dfrac{bc}{b\left(b+c\right)}\)
Theo đề bài \(\dfrac{a}{b}< 1\) suy ra \(a< b\) nên \(ac< bc\). Do đó \(\dfrac{ac}{b\left(b+c\right)}< \dfrac{bc}{b\left(b+c\right)}\)
Suy ra \(\dfrac{a}{b}< \dfrac{a+c}{b+c}\)
1N
Cho \(a,b,c\in N.\) Giải thích tại sao, nếu \(\dfrac{a}{b}>1\) thì \(\dfrac{a}{b}>\dfrac{a+c}{b+c}\)
5
9 tháng 5 2022
Biến đổi `:`
`a/b > ( a + c )/( b + c )`
`<=> a( b + c ) > b( a + c )`
`<=> ab + ac > ab + bc`
`<=> ab+ac-ab>ab+bc-ab`
`<=> ac>bc`
`<=> ( ac )/( bc ) = a/b > 1` `(` luôn đúng `)`
9 tháng 5 2022
\(\dfrac{a}{b}=\dfrac{a\left(b+c\right)}{b\left(b+c\right)}=\dfrac{ab}{b\left(b+c\right)}+\dfrac{ac}{b\left(b+c\right)};\dfrac{a+c}{b+c}=\dfrac{b\left(a+c\right)}{b\left(b+c\right)}=\dfrac{ab}{b\left(b+c\right)}+\dfrac{bc}{b\left(b+c\right)}\)
Ta có \(\dfrac{a}{b}>1,\) suy ra \(a>b\) nên ac > bc. Do đó, \(\dfrac{ac}{b\left(b+c\right)}>\dfrac{bc}{b\left(b+c\right)}\), suy ra \(\dfrac{a}{b}>\dfrac{a+c}{b+c}\)
HG
1
H9
HT.Phong (9A5)
CTVHS
19 tháng 8 2023
a) Ta có:
\(CD\perp AD\)
\(AB\perp AD\)
\(\Rightarrow CD//AB\)
b) Ta có:
\(AB//CD\)
Nên: \(\widehat{B}+\widehat{C}=180^o\)
Do hai góc này ở vị trí trong cùng phía
BL
9 tháng 5 2021
a) Xét ABD và EBD có
BD cạnh chung
BAD=BED(=90)
ABD=EBD(vì BD là tia phân giác của B)
b ko biet
BL
9 tháng 5 2021
b)Vì theo ý a) BAD=BED và BD là tia phân giác của B. Nên ADE là tam giác cân
(-c)(-b)=bc