(x2-3)2 = 16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 9 2023
Để olm giúp em em nhé!
a, \(\dfrac{x+2}{7x+42}\) = \(\dfrac{x+2}{7.\left(x+6\right)}\) = \(\dfrac{\left(x+2\right)\left(x-6\right)}{7\left(x-6\right)\left(x+6\right)}\) (đk \(x\ne\) \(\mp\) 6)
\(\dfrac{-13x}{x^2-36}\) = \(\dfrac{-13x}{\left(x-6\right)\left(x+6\right)}\) = \(\dfrac{-7.13.x}{7.\left(x-6\right).\left(x+6\right)}\) = \(\dfrac{-91x}{7.\left(x-6\right)\left(x+6\right)}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 9 2023
b, \(\dfrac{7}{4x+16}\) = \(\dfrac{7\left(x-4\right)}{4.\left(x+4\right).\left(x-4\right)}\) (đk \(x\ne\) \(\pm\) 4)
\(\dfrac{15}{x^2-16}\) = \(\dfrac{15.4}{\left(x-4\right)\left(x+4\right).4}\) = \(\dfrac{60}{4.\left(x-4\right).\left(x+4\right)}\)
DD
1
20 tháng 7 2023
b) \(\left(x-1\right)\left(x^2+x+1\right)-x\left(x-3\right)\left(x+3\right)=8\)
\(\Rightarrow x^3-1-x\left(x^2-9\right)=8\)
\(\Rightarrow x^3-1-x^3+9x=8\)
\(\Rightarrow9x=9\Rightarrow x=1\)
c) \(\left(x^2+2\right)\left(x-4\right)-\left(x+2\right)\left(x^2+4x+4\right)=-16\)
\(\Rightarrow x^3-4x^2+2x-8-\left(x+2\right)\left(x+2\right)^2=-16\)
\(\Rightarrow x^3-4x^2+2x-8-\left(x+2\right)^3=-16\)
\(\Rightarrow x^3-4x^2+2x-8-\left(x^3+6x^2+12x+8\right)=-16\)
\(\Rightarrow x^3-4x^2+2x-8-x^3-6x^2-12x-8=-16\)
\(\Rightarrow-10x^2-10x-16=-16\)
\(\Rightarrow10x^2+10x=0\)
\(\Rightarrow10x\left(x+1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
26 tháng 10 2021
a: \(\Leftrightarrow\left(x-3\right)\left(5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)
b: \(\Leftrightarrow x\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
CM
24 tháng 9 2018
a) Rút gọn được VT = 9x + 7. Từ đó tìm được x = 1.
b) Rút gọn được VT = 2x + 8. Từ đó tìm được x = 7 2 .
H9
HT.Phong (9A5)
CTVHS
29 tháng 10 2023
a) \(\left(2x+3y\right)^2=\left(2x\right)^2+2\cdot2x\cdot3y+\left(3y\right)^2=4x^2+12xy+9y^2\)
b) \(\left(x+\dfrac{1}{4}\right)^2=x^2+2\cdot x\cdot\dfrac{1}{4}+\left(\dfrac{1}{4}\right)^2=x^2+\dfrac{1}{2}x+\dfrac{1}{16}\)
c) \(\left(x^2+\dfrac{2}{5}y\right)\left(x^2-\dfrac{2}{5}y\right)=\left(x^2\right)^2-\left(\dfrac{2}{5}y\right)^2=x^4-\dfrac{4}{25}y^2\)
d) \(\left(2x+y^2\right)^3=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y^2+3\cdot2x\cdot\left(y^2\right)^2+\left(y^2\right)^3=8x^3+12x^2y^2+6xy^4+y^6\)
e) \(\left(3x^2-2y\right)^2=\left(3x^2\right)^2-2\cdot3x^2\cdot2y+\left(2y\right)^2=9x^4-12x^2y+4y^2\)
f) \(\left(x+4\right)\left(x^2-4x+16\right)=x^3+4^3=x^3+64\)
g) \(\left(x^2-\dfrac{1}{3}\right)\cdot\left(x^4+\dfrac{1}{3}x^2+\dfrac{1}{9}\right)=\left(x^2\right)^3-\left(\dfrac{1}{3}\right)^3=x^6-\dfrac{1}{27}\)
30 tháng 7 2021
1)(x2-4x+16)(x+4)-x(x+1)(x+2)+3x2=0
\(\Rightarrow\)(x3+64)-x(x2+2x+x+2)+3x2=0
\(\Rightarrow\)x3+64-x3-2x2-x2-2x+3x2=0
\(\Rightarrow\)-2x+64=0
\(\Rightarrow\)-2x=-64
\(\Rightarrow\)x=\(\dfrac{-64}{-2}\)
\(\Rightarrow x=32\)
30 tháng 7 2021
2)(8x+2)(1-3x)+(6x-1)(4x-10)=-50
\(\Rightarrow\)8x-24x2+2-6x+24x2-60x-4x+10=50
\(\Rightarrow\)-62x+12=50
\(\Rightarrow\)-62x=50-12
\(\Rightarrow\)-62x=38
\(\Rightarrow\)x=\(-\dfrac{38}{62}=-\dfrac{19}{31}\)
CM
10 tháng 7 2017
a) TXĐ: R
y′ = 6x − 24 x 2 = 6x(1 − 4x)
y' = 0 ⇔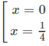 
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng ( - ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng ( - ∞ ;0 ); (14; + ∞ )
b) TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔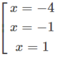 
Bảng biến thiên:
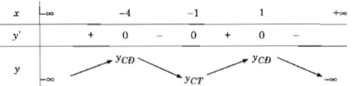
Vậy hàm số y đã cho đồng biến trên các khoảng ( - ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
c) TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng ( - ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng ( - ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔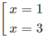 
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng ( - ∞ ; 0) ⇒ y nghịch biến trên khoảng ( - ∞ ; 0)
=> x^2-3=4
x^2=7
=. x= căn 7 hoặc âm căn 7
\(\left(x^2-3\right)^2=16=4^2\)
=>\(x^2-3=4\)hoac \(x^2-3=-4\)