cho 9 điểm không có 3 điểm nào thẳng hàng nằm trong tam giác abc . Chứng minh: có một tam giác diện tích < 1/4 diện tích tam giác abc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 5 2016
Gọi M,N,P lần lượt là trung điểm các cạnh AB,AC,BC
Do đó diện tích AMN = diện tích BMP = diện tích ANP = \(\frac{1}{4}\) diện tích ABC
Theo nguyên lý di - rich - le thì trong 9 điểm đề bài cho,ít nhất có 3 điểm nằm trong tam giác AMN,BMP hoặc tam giác ANP
Gọi 3 điểm đó là H,I,K
Chẳng hạn 3 điểm H,I,K nằm trong tam giác ANP
= > diện tích HIK < diện tích ANP = \(\frac{1}{4}\) diện tích tam giác ABC
Vậy sẽ có một tam giác nhỏ hơn \(\frac{1}{4}\) diện tích tam giác ABC
Đáp số : Sẽ có một tam giác nhỏ hơn \(\frac{1}{4}\) diện tích tam giác ABC
PN
17 tháng 5 2016
Gọi M ,N ,P lần lượt là trung điểm các cạnh AB ,AC , BC . Do đó \(S_{AMN}=S_{BMP}=S_{ANP}=\frac{1}{4}S_{ABC}\)
Theo nguyên lí di-rich-le thì trong chín điểm đề bài cho, có ít nhất ba điểm nằm trong tam giác AMN,BMP,ANP gọi 3 điểm đó là H , I , K
chẳng hạn 3 điểm H,I,K nằm trong ANP
\(\Rightarrow S_{HIK}< S_{ANP}=\frac{1}{4}S_{ABC}\)
Vậy sẽ có một tâm giác nhỏ hơn 1/4 diện tích tam giác ABC
7 tháng 3 2020
làm sao cho chữ màu cam cam zậy bạn???
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 7 2023
\(\dfrac{1}{2}\)SBCD = \(\dfrac{2}{3}\)SADC
Diện tích tam giác BCD bằng: \(\dfrac{2}{3}\): \(\dfrac{1}{2}\) = \(\dfrac{4}{3}\)(diện tích tam giác ADC)
\(\dfrac{3}{4}\)SABD = \(\dfrac{2}{3}\)SACD
Diện tích ABD bằng: \(\dfrac{2}{3}\): \(\dfrac{3}{4}\) = \(\dfrac{8}{9}\)(diện tích tam giác ADC)
232 cm2 ứng với phân số là:
1 + \(\dfrac{4}{3}\) + \(\dfrac{8}{9}\) = \(\dfrac{29}{9}\) (diện tích tam giác ADC)
Diện tích tam giác ADC là:
232 : \(\dfrac{29}{9}\) = 72 (cm2)
Diện tích tam giác BCD là: 72 \(\times\) \(\dfrac{4}{3}\) = 96 (cm2)
Diện tích tam giác ABD là: 72 \(\times\)\(\dfrac{8}{9}\) = 64 (cm2)
Đáp số: ....
CM
2 tháng 9 2019
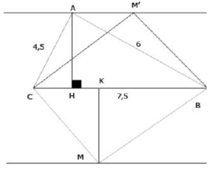
a) Ta có: A B 2 + A C 2 = 6 2 + 4 , 5 2 = 7 , 5 2 = B C 2
nên tam giác ABC vuông tại A. (đpcm)
= > ∠ B = 37 ° = > ∠ C = 90 ° - ∠ B = 90 ° - 37 ° = 53 °
Mặt khác trong tam giác ABC vuông tại A, ta có:
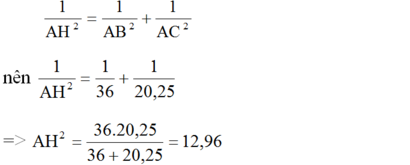
=> AH = 3,6 cm
b) Gọi khoảng cách từ M đến BC là MK. Ta có:
Ta thấy SMBC = SABC khi MK = AH = 3,6 cm
Do đó để SMBC = SABC thì M phải nằm trên đường thẳng song song và cách BC một khoảng là 3,6 cm (có hai đường thẳng như trên hình).
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 8 2023
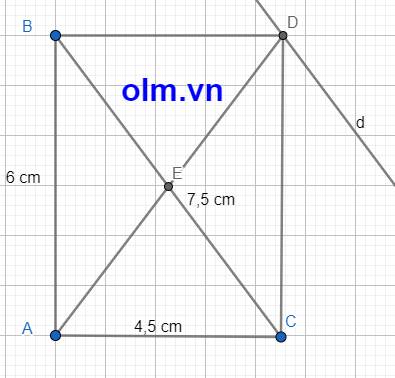
a, Xét \(\Delta\)ABC có: AB2 + AC2 = 62 + 4,52 = 56,25 (cm2)
BC2 = 7,52 = 56,25 (cm2)
AB2 + AC2 = BC2 vậy tam giác ABC vuông tại A (đpcm)
SinC = 6 : 7,5 =0,8 ⇒ \(\widehat{C}\) = 53,130 ⇒ \(\widehat{B}\) = 900 - 53,130 = 36,870
b, Dựng hình chữ nhật ABCD, chiều cao AH, DK, và đường thẳng d đi qua D song song với BC như hình vẽ ta có
SABC = SBDC ⇒ AH = DK
Lây 1 điểm bất M kỳ di động trên đường thẳng d ta có:
SBDC = SMBC (vì hai tam giác có chiều cao bằng nhau và chung cạnh đáy BC)
⇒ SABC = SMBC
Kết luận khi M di động trên đường thẳng d thì diện tích tam giác MBC luôn bằng diện tích tam giác ABC
gọi M,N,P lần lượt là trung điểm các cạnh AB,AC,BC
do đó SAMN=SBMP=SANP=1/4 SABC
theo nguyên lý di-rich-le thì trong chín điểm đề bài cho, có ít nhất 3 điểm nằm trong tam giác AMN,BMP hoặc tam giác ANP
gọi 3 điểm đó là H,I,K
chẳng hạn 3 điểm H,I,K nằm trong tam giác ANP
=> SHIK<SANP=1/4 SABC
vậy sẽ có một tam giác nhỏ hơn 1/4 diện tích tam giác ABC
đúng cho mình cái nha!!!
Cho mik hỏi cho tam giác ABC,M là chung điểm của AB,N là chung điểm của AC.So SMNBC với SABC