cứu tìm y ạ huhu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1
a) \(2^{11}.64=2^{11}.2^6=2^{17}\)
Do \(16< 17\Rightarrow2^{16}< 2^{17}\)
Vậy \(2^{16}< 2^{11}.64\)
b) Do \(18>17\Rightarrow9^{18}>9^{17}\) (1)
\(9^{18}=\left(3^2\right)^{18}=3^{36}\)
Do \(36< 37\Rightarrow3^{36}< 3^{37}\)
\(\Rightarrow9^{18}< 3^{37}\) (2)
Từ (1) và (2) \(\Rightarrow9^{17}< 3^{37}\)
c) \(2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{222}=\left(3^2\right)^{111}=9^{111}\)
Do \(8< 9\Rightarrow8^{111}< 9^{111}\)
Vậy \(2^{333}< 3^{222}\)
d) \(3^{50}=\left(3^2\right)^{25}=9^{25}\)
Do \(9< 11\Rightarrow9^{25}< 11^{25}\)
Vậy \(3^{50}< 11^{25}\)
e) \(37< 38\Rightarrow3^{37}< 3^{38}\) (1)
Lại có: \(3^{38}=3^{2.19}=\left(3^2\right)^{19}=9^{19}\)
Do \(9< 10\Rightarrow9^{19}< 10^{19}\)
\(\Rightarrow3^{38}< 10^{19}\) (2)
Từ (1) và (2) \(\Rightarrow3^{37}< 10^{19}\)
f) Do \(17>16\Rightarrow17^{14}>16^{14}\) (1)
Do \(32>31\Rightarrow32^{11}>31^{11}\) (2)
Lại có:
\(16^{14}=\left(2^4\right)^{14}=2^{56}\)
\(32^{11}=\left(2^5\right)^{11}=2^{55}\)
Do \(56>55\Rightarrow2^{56}>2^{55}\)
\(\Rightarrow16^{14}>32^{11}\) (3)
Từ (1), (2) và (3) \(\Rightarrow17^{14}>31^{11}\)
Bài 2:
a) \(2^n-64=0\)
\(2^n=64\)
\(2^n=2^6\)
\(n=6\)
b) \(5.3^{n-3}-405=0\)
\(5.3^{n-3}=405\)
\(3^{n-3}=405:5\)
\(3^{n-3}=81\)
\(n-3=4\)
\(n=4+3\)
\(n=7\)
c) \(4^n.8=2^{15}\)
\(\left(2^2\right)^n.2^3=2^{15}\)
\(2^{2n}.2^3=2^{15}\)
\(2^{2n+3}=2^{15}\)
\(2n+3=15\)
\(2n=15-3\)
\(2n=12\)
\(n=12:2\)
\(n=6\)
d) \(3.2^{n+1}+2^{n+2}=160\)
\(2^{n+1}.\left(3+2\right)=160\)
\(2^{n+1}.5=160\)
\(2^{n+1}=160:5\)
\(2^{n+1}=32\)
\(2^{n+1}=2^5\)
\(n+1=5\)
\(n=5-1\)
\(n=4\)

Giải:
Ta có: \(3\left(x-1\right)=2\left(y-2\right)\Rightarrow\frac{x-1}{2}=\frac{y-2}{3}\)
\(4\left(y-2\right)=3\left(z-3\right)\Rightarrow\frac{y-2}{3}=\frac{z-3}{4}\)
\(\Rightarrow\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\frac{2x-2}{4}=\frac{3y-6}{9}=\frac{z-3}{4}=\frac{2x-2+3y-6+z-3}{4+9+4}=\frac{\left(2x+3y+z\right)-\left(2+6+3\right)}{17}\)
\(=\frac{50-11}{17}=\frac{39}{17}\)
+) \(\frac{x-1}{2}=\frac{39}{17}\Rightarrow x-1=\frac{78}{17}\Rightarrow x=\frac{95}{17}\)
+) \(\frac{y-2}{3}=\frac{39}{17}\Rightarrow y-2=\frac{117}{17}\Rightarrow y=\frac{151}{17}\)
+) \(\frac{z-3}{4}=\frac{39}{17}\Rightarrow z-3=\frac{156}{17}\Rightarrow z=\frac{207}{17}\)
Vậy bộ số \(\left(x;y;z\right)\) là \(\left(\frac{95}{17};\frac{151}{17};\frac{207}{17}\right)\)
Pn giỏi wa mk còn tận 2 bài nữa bn có sẵn lòng giúp mk hk ??





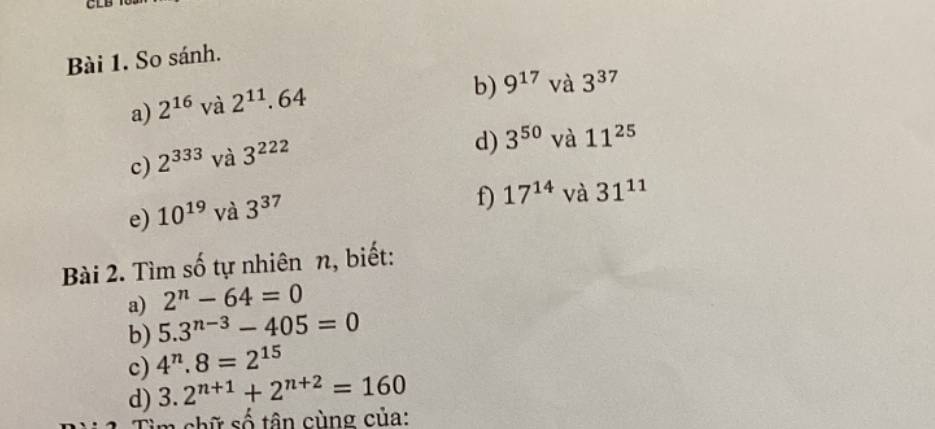






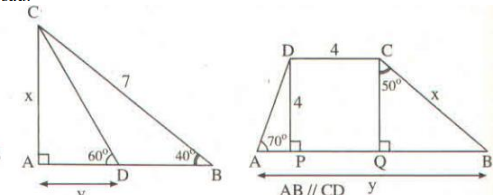
Xét ΔABC có MN//BC
nên AM/MB=AN/NC
=>4/x=3/2
=>x=8/3(cm)
=>AB=8/3+4=20/3(cm)
Xét ΔBAC có BN là phân giác
nên BC/BA=NC/AN
=>y:20/3=2/3
=>y=2/3*20/3=40/9(cm)