Cho tứ diện ABCD có A(0;1;-1), B(1;1;2), C(1;-1;0), D(0;0;1). Tính độ dài đường cao AH của hình chóp ABCD.
A. 3 2
B. 2 2
C. 2 2
D. 3 2 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
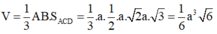
Phương án nhiễu.
A. Sai vì 2 cách: một là thấy số 1 3 cứ chọn, hai là trong công thức thể tích thiếu 1 3 diện tích đáy.
C. Sai vì thiếu 1 3 trong công thức thể tích.

Đáp án A.
Với mỗi cách chọn ra 2 đỉnh bất kỳ của tứ diện ta được 2 vecto đối nhau.
Do đó có 2 C 4 2 = 12 vecto.

Đáp án là B
Mỗi cạnh của tứ diện tạo thành 2 vecto thỏa mãn đề bài, suy ra có 6.2 = 12 vecto.

Đáp án B.
Mỗi cạnh của tứ diện tạo thành 2 vecto thỏa mãn đề bài, suy ra có 6.2=12 vecto

Chọn A
Số vectơ khác vectơ 0 → mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD là số các chỉnh hợp chập 2 của phần tử => số vectơ là A 4 2 = 12

Đáp án A.
Với mỗi cách chọn ra 2 đỉnh bất kỳ của tứ diện ta được 2 vecto đối nhau.
Do đó có 2 C 4 2 = 12 vecto.

Đáp án B
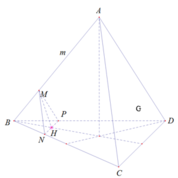
Trong (ABC) kẻ MN // AC ( N ∈ BC)
Trong (ABD) kẻ MP // AD ( P ∈ BD)
⇒ (MNP) là mặt phẳng cần tìm
Xét tam giác MNP có MN = MP =NP (= a - m )
⇒ tam giác MNP đều
Mà NP // CD và BG là trung tuyến tam giác BCD
⇒ BG cắt NP tại H là trung điểm NP
⇒ MH là đường cao tam giác MNP
Ta có: PH = a - m 2 và MP = a – m. Áp dụng định lý pitago, ta có: MH = 3 2 a - m
Và NP = a – m
SMNP = MH . NP 2 = 3 4 a - m 2
Đáp án là D