Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Với mỗi cách chọn ra 2 đỉnh bất kỳ của tứ diện ta được 2 vecto đối nhau.
Do đó có 2 C 4 2 = 12 vecto.

Đáp án D
Với hai đỉnh bất kì trong 6 đỉnh đã cho tạo được 2 vecto. Số vecto cần tính là A 6 2

Chọn B
Gọi I là trung điểm AB, J là trung điểm CD
Từ AC=AD=BC=BD =>IJ chính là đoạn vuông góc chung của 2 đường thẳng AB và CD
=> IJ = a
Gọi O là điểm cách đều 4 đỉnh => O là tâm mặt cầu ngoại tiếp tứ diện ABCD
=> O nằm trên IJ => Ta cần tính OA
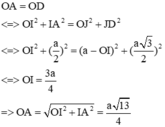
Ta có:

Đáp án C

Khối bát diện đều có cạnh là a.
Chia bát diện đều thành hai hình chóp tứ giác đều có tất cả các cạnh bằng a.
Thể tích khối chóp tứ giác đều S.MNPQ là
V S . M N P Q = 1 3 d S ; M N P Q . S M N P Q = 1 3 . a 2 − a 2 2 . a 2 = a 3 2 6
Vậy thể tích cần tính là:
V = 2 x V S . M N P Q = 2. a 3 2 6 = a 3 2 3 .



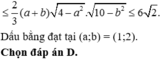

Đáp án là B
Mỗi cạnh của tứ diện tạo thành 2 vecto thỏa mãn đề bài, suy ra có 6.2 = 12 vecto.