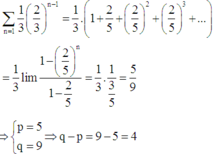nếu tung một đồng xu 10 lần mà 10 lần đều là mặt sấp thì ở lần tung thứ 11 xác suất tung được mặt sấp là bao nhiêu ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xác suất thực nghiệm của biến cố hai đồng xu đều xuất hiện mặt sấp sau 100 lần gieo là \(\frac{{14}}{{100}} = \frac{7}{{50}}\).
Vậy suất thực nghiệm của biến cố hai đồng xu đều xuất hiện mặt sấp sau 100 lần gieo là \(\frac{7}{{50}}\).

- Biến cố A là biến cố chắc chắn xảy ra vì hai lần tung đều xuất hiện mặt sấp.
- Biến cố B là biến cố chắc chắn xảy ra vì 2 lần đều xuất hiện mặt sấp giống nhau.
- Biến cố C là biến cố không thể vì cả 2 lần đều xuất hiện mặt sấp nên không thể ra mặt ngửa.

a, Xác suất thực nghiệm xuất hiện mặt N là:\(\frac{13}{22}\)
b,Xác suất thực nghiệm xuất hiện mặt S là:\(\frac{11}{25}\)
c,Số lần xuất hiện mặt S là: 30 - 14 = 16
,Xác suất thực nghiệm xuất hiện mặt S là:\(\frac{16}{30}\)

+) Không gian mẫu trong trò chơi trên là tập hợp \(\Omega = {\rm{ }}\left\{ {SS;{\rm{ }}SN;{\rm{ }}NS;{\rm{ }}NN} \right\}\). Vậy \(n\left( \Omega \right) = 4\)
+) Gọi A là biến cố “Có ít nhất một lần xuất hiện mặt sấp”
+) Các kết quả thuận lợi cho biến cố A là: \(SS;{\rm{ }}SN;{\rm{ }}NS\)tức là \(A = {\rm{ }}\left\{ {SS;{\rm{ }}SN;{\rm{ }}NS} \right\}\). Vậy \(n\left( A \right) = 3\).
+) Xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{3}{4}\)

Vì tung đồng xu 20 lần mà có 12 lần mặt ngửa nên có 8 mặt sấp.
Xác suất của biến cố ''Tung được mặt sấp'' là: \(\dfrac{8}{20}=\dfrac{2}{5}\)
Đáp số: `2/5`.
Do đó: không có đáp án nào đúng cả.

a)
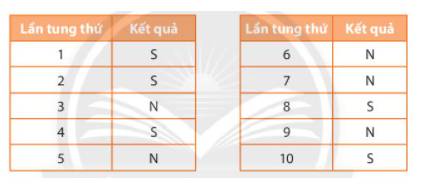
- Bạn Hùng đã tung đồng xu 10 lần. Kết quả của lần thứ nhất là mặt sấp, lần thứ năm là mặt ngửa.
- Có 2 kết quả khác nhau có thể xảy ra, đó là kết quả đồng xu hiện ra mặt sấp hoặc đồng xu hiện ra mặt ngửa.
b)
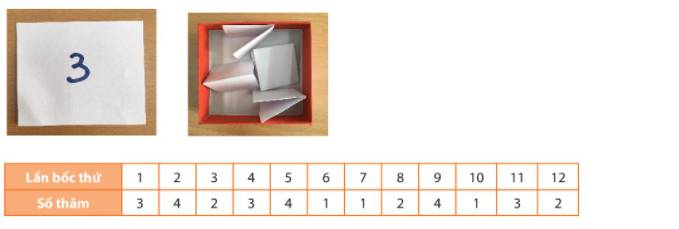
- Kết quả lần thứ 5 là số 4, lần thứ 6 là số 1.
- Có 4 kết quả khác nhau có thể xảy ra, đó là các kết quả 1,2,3,4.

Đáp án B
Phương pháp: Nhân xác suất.
Cách giải: Gọi số lần Amelia tung đồng xu là n , ( n ∈ N * ) => Số lần Blaine tung là n - 1
Amelia thắng ở lần tung thứ n của mình nên n - 1 lượt đầu Amelia tung mặt sấp, lần thứ n tung mặt ngửa, còn toàn bộ n - 1 lượt của Blaine đều sấp. Khi đó:
Xác suất Amelia thắng ở lần tung thứ n:
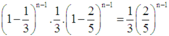
Xác suất Amelia thắng :