Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xác suất thực nghiệm của biến cố ngẫu nhiên "Mặt xuất hiện của đồng xu là mặt N" là \(\dfrac{8}{15}\)
Xác suất thực nghiệm này bằng với xác suất của biến cố ngẫu nhiên ở trên

a) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của đồng xu là mặt S" là: `27/50`
b) Khi tung đồng xu 45 lần liên tiếp, do mặt N xuất hiện 24 lần nên mặt S xuất hiện 21 lần. Do đó, xác suất thực nghiệm của biến cố "Mặt xuất hiện của đồng xu là mặt S" là: `21/50`

Số lần xuất hiện mặt sấp là: 40 - 19 = 21
Xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” là \(\frac{{21}}{{40}}\).

Khi tung một đồng xu, có hai kết quả có thể xảy ra là mặt sấp và mặt ngửa.
Gọi \(A\) là biến cố xuất hiện mặt sấp.
Khi đó, xác suất xảy ra biến cố \(A\) là:
\(P\left( A \right) = \frac{1}{2}\).
Gieo 100 lần thì theo lí thuyết sẽ có 50 lần xuất hiện mặt sấp.
Vì số lần thử là 100 đủ lớn nên xác xuất thực nghiệm sẽ càng gần với \(P\left( A \right)\).
Do đó, khả năng đoán đúng của bạn Thúy cao hơn.

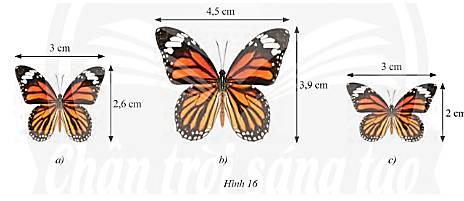
- Xét hình 16a và hình 16b ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 16a và hình 16b lần lượt là:
\(\frac{3}{{4,5}} = \frac{2}{3};\frac{{2,6}}{{3,9}} = \frac{2}{3}\). Do đó, tồn tại hình động dạng phối cảnh của hình 16a bằng hình 16b. Do đó, hình 16a và hình 16b đồng dạng với nhau.
- Xét hình 16b và hình 16c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 16b và hình 16c lần lượt là:
\(\frac{{4,5}}{3} = 1,5;\frac{{3,9}}{2} = 1,95\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 16b để bằng hình 16c. Do đó, hình 16b và hình 16c không đồng dạng với nhau.
- Xét hình 16c và hình 16c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 16a và hình 16c lần lượt là:
\(\frac{3}{3} = 1;\frac{{2,6}}{2} = 1,3\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 16a để bằng hình 16c. Do đó, hình 16a và hình 16c không đồng dạng với nhau.

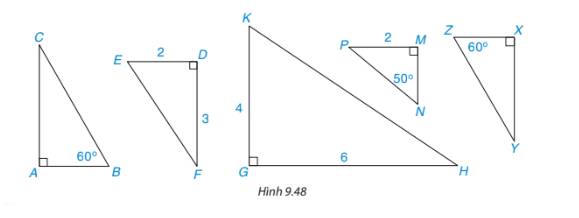
Các cặp tam giác vuông đồng dạng:
\(\begin{array}{l}\Delta ABC \backsim \Delta X{\rm{Z}}Y(\widehat A = \widehat X;\widehat B = \widehat Z)\\\Delta E{\rm{D}}F \backsim \Delta KGH\left( {\frac{{E{\rm{D}}}}{{KG}} = \frac{{DF}}{{GF}};\widehat {E{\rm{D}}F} = \widehat {KGH}} \right)\end{array}\)




Xác suất thực nghiệm của biến cố hai đồng xu đều xuất hiện mặt sấp sau 100 lần gieo là \(\frac{{14}}{{100}} = \frac{7}{{50}}\).
Vậy suất thực nghiệm của biến cố hai đồng xu đều xuất hiện mặt sấp sau 100 lần gieo là \(\frac{7}{{50}}\).