Cho T = 3a 2 + 6ab + 3b 2 a + b và a + b = 3. Khi đó?
A. T = 27
B. T = 3
C. T = 9
D. T = 18
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
13 tháng 6 2018
Đúng(0)
Những câu hỏi liên quan
NT
1
CN
12 tháng 7 2018
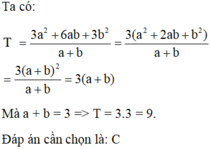
a) 2x2 - 28x + 98
= 2.(x2 - 2.x.7 + 72)
= 2.(x - 7)2
b) 5x2 - 20y2
= 5.[x2 - (2y)2 ]
= 5.(x - 2y).(x + 2y)
c) 4x2 - 324
= 4.(x2 - 92)
= 4.(x - 9).(x + 9)
d) 3a2 + 6ab + 3b2
= 3.(a2 + 2ab + b2)
= 3.(a + b)2
e) (a - 4)2 - 4y2
= (a - 4)2 - (2y)2
= (a - 2y - 4).(a + 2y - 4)
f) 2x3 + 16
= 2.(x3 + 23)
= 2.(x + 2).(x2 + 2x + 4)
KB
27 tháng 8 2018
a ) \(x^3+3x^2+6x+4\)
\(=x^3+3x^2+3x+1+3x+3\)
\(=\left(x+1\right)^3+3\left(x+1\right)\)
\(=\left(x+1\right)\left[\left(x+1\right)^2+3\right]\)
\(=\left(x+1\right)\left(x^2+2x+4\right)\)
b ) \(3a^2c^2+bd+3abc+acd\)
\(=\left(3a^2c^2+3abc\right)+\left(bd+acd\right)\)
\(=3ac\left(ac+b\right)+d\left(ac+b\right)\)
\(=\left(3ac+d\right)\left(ac+b\right)\)
c ) \(3a^2-6ab+3b^2-12c^2\)
\(=3\left(a^2-2ab+b^2\right)-3\left(2c\right)^2\)
\(=3\left[a^2-2ab+b^2-\left(2c\right)^2\right]\)
\(=3\left[\left(a-b\right)^2-\left(2c\right)^2\right]\)
\(=3\left(a-b-2c\right)\left(a-b+2c\right)\)
d ) \(x^2+y^2-x^2y^2+xy-x-y\)
\(=-x^2y^2+x^2+y^2-y+xy-x\)
\(=-x^2\left(y^2-1\right)+y\left(y-1\right)+x\left(y-1\right)\)
\(=-x^2\left(y+1\right)\left(y-1\right)+\left(x+y\right)\left(y-1\right)\)
\(=\left(y-1\right)\left[-x^2\left(y+1\right)+x+y\right]\)
\(=\left(y-1\right)\left[-x^2y-x^2+x+y\right]\)
\(=\left(y-1\right)\left[x\left(1-x\right)+y\left(1-x^2\right)\right]\)
\(=\left(y-1\right)\left[x\left(1-x\right)+y\left(1+x\right)\left(1-x\right)\right]\)
\(=\left(y-1\right)\left[x+y\left(1+x\right)\right]\left(1-x\right)\)
e ) \(a^6-b^6=\left(a^3\right)^2-\left(b^3\right)^2=\left(a^3-b^3\right)\left(a^3+b^3\right)\) \(=\left(a-b\right)\left(a^2+ab+b^2\right)\left(a+b\right)\left(a^2-ab+b^2\right)\)
27 tháng 8 2018
a, \(x^3+3x^2+6x+4\)
\(=\left(x^3+x^2\right)+\left(2x^2+2x\right)+\left(4x+4\right)\)
\(=x^2\left(x+1\right)+2x\left(x+1\right)+4\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+2x+4\right)\)
KN
29 tháng 9 2017
a) x3 - 4x2 + 4x
= x(x2 - 4x + 4)
= x(x - 2)2
b) 2xy - x2 - y2 + 16
= 16 -x2 + 2xy - y2
= 16 - (x2 - 2xy + y2)
= 42 - (x - y)2
= [4 - (x - y)].(4 + x - y)
= (4 - x + y)(4 + x - y)
c) x2 - y2 - 2yz - z2
= x2 - (y2 + 2yz + z2)
= x2 - (y + z)2
= [x -(y + z)].(x + y +z)
=(x - y - z)(x + y + z)
d) 3a2 - 6ab + 3b2 - 12c2
= 3(a2 - 2ab + b2 - 4c2)
= 3[(a2 - 2ab + b2) - (2c)2]
= 3[(a - b)2 - (2c)2]
= 3(a - b - c)(a - b + c)
con D bạn chép sai đề bài rồi, phải là +3b2 chứ. tích cho mik nha, ko thì lần sau mik ko giúp đâu ihihihi.....!!!!!!!!!
22 tháng 11 2017
\(3a^2+3b^2=10ab\)
\(\Rightarrow3a^2-10ab+3b^2=0\)
\(\Rightarrow3a^2-ab-9ab+3b^2=0\)
\(\Rightarrow\left(3a^2-ab\right)-\left(9ab-3b^2\right)=0\)
\(\Rightarrow a\left(3a-b\right)-3b\left(3a-b\right)=0\)
\(\Rightarrow\left(3a-b\right)\left(a-3b\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3a-b=0\\a-3b=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}b=-3a\\b=\dfrac{a}{3}\end{matrix}\right.\)
Với \(b=-3a,\)có :
\(P=\dfrac{-3a-a}{-3a+a}=\dfrac{-4a}{-2a}=2\)
Với \(b=\dfrac{a}{3},\)có :
\(P=\dfrac{\dfrac{a}{3}-a}{\dfrac{a}{3}+a}=\dfrac{\dfrac{a}{3}-\dfrac{3a}{3}}{\dfrac{a}{3}+\dfrac{3a}{3}}=\dfrac{-\dfrac{2a}{3}}{\dfrac{4a}{3}}=-\dfrac{2a}{3}.\dfrac{3}{4a}=-\dfrac{1}{2}\)
( Nếu sai thì cho mk xin lỗi nha bn , tại mk ko chắc lắm )