Cho a > 0, b > 0 va a + b = 1. Tìm giá trị nhỏ nhất của biểu thức Q = a 3 + b 3 + 4 a b − a b .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
27 tháng 7 2018
Đúng(0)
Những câu hỏi liên quan
2 tháng 8 2019
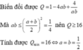
\(M=\left(a^2+\frac{1}{16a^2}\right)+\left(b^2+\frac{1}{16b^2}\right)+\frac{15}{16}\left(\frac{1}{a^2}+\frac{1}{b^2}\right)\)
\(\ge2\sqrt{\frac{a^2}{16a^2}}+2\sqrt{\frac{b^2}{16b^2}}+\frac{15\left(\frac{1}{a}+\frac{1}{b}\right)^2}{32}\ge1+\frac{\frac{240}{\left(a+b\right)^2}}{32}\ge\frac{17}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(a=b=\frac{1}{2}\)
DX
1
TD
1
27 tháng 4 2017
Áp dụng bđt \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge\frac{9}{x+y+z}\forall x;y;z\ge0\) ta được :
\(B=\frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}\ge\frac{9}{3+\left(a+b+c\right)}=\frac{9}{3+3}=\frac{9}{6}=\frac{3}{2}\)
Dấu "=" xảy ra <=> \(a=b=c=1\)
Vậy GTNN của B là \(\frac{3}{2}\) tại \(a=b=c=1\)
31 tháng 5 2018
Ta thấy: \(a+b\le1\Leftrightarrow\hept{\begin{cases}a\le1-b\\b\le1-a\end{cases}}\Leftrightarrow\hept{\begin{cases}1+a\le2-b\\1+b\le2-a\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{1+b}\ge\frac{a}{2-a}\\\frac{b}{1+a}\ge\frac{b}{2-b}\end{cases}}\Rightarrow\frac{a}{1+b}+\frac{b}{1+a}\ge\frac{a}{2-a}+\frac{b}{2-b}\)
\(\Rightarrow S=\frac{a}{1+b}+\frac{b}{1+a}+\frac{1}{a+b}\ge\frac{a}{2-a}+\frac{b}{2-b}+\frac{1}{a+b}\)
\(=\frac{2}{2-a}-1+\frac{2}{2-b}-1+\frac{1}{a+b}=\frac{2}{2-a}+\frac{2}{2-b}+\frac{1}{a+b}-2\)
\(=2\left(\frac{1}{2-a}+\frac{1}{2-b}+\frac{1}{2\left(a+b\right)}-1\right)\)
Áp dụng bất đẳng thức sau: \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge\frac{9}{x+y+z}\)
\(\Rightarrow\frac{1}{2-a}+\frac{1}{2-b}+\frac{1}{2\left(a+b\right)}\ge\frac{9}{4-\left(a+b\right)+2\left(a+b\right)}=\frac{9}{4+a+b}\)
Lại có: \(a+b\le1\Rightarrow4+a+b\le5\Rightarrow\frac{9}{4+a+b}\ge\frac{9}{5}\)
\(\Rightarrow\frac{1}{2-a}+\frac{1}{2-b}+\frac{1}{2\left(a+b\right)}\ge\frac{9}{5}\Leftrightarrow2\left(\frac{1}{2-a}+\frac{1}{2-b}+\frac{1}{2\left(a+b\right)}-1\right)\ge\frac{8}{5}\)
\(\Rightarrow S\ge\frac{8}{5}.\)
Vậy \(Min_S=\frac{8}{5}.\)Dấu "=" xảy ra khi \(a=b=\frac{2}{5}.\)
LP
0
TD
1
XO
29 tháng 5 2021
Ta có \(\frac{a}{b}+\frac{b}{a}\ge2\)
=> \(\frac{a^2+b^2}{ab}\ge2\)
=> a2 + b2 \(\ge\)2ab
=> a2 + b2 - 2ab\(\ge\)0
=> (a - b)2 \(\ge\)0 (đúng)
Dấu "=" xảy ra <=> a - b = 0 => a = b
=> Bất đẳng thức được chứng minh
XO
29 tháng 5 2021
P = \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
=> \(\left(a+b+c\right).P=\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
=> \(3P=1+\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+1+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}+1\)
=> \(3P=3+\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{b}{a}+\frac{a}{b}\right)\ge3+2+2+2=9\left(cmt\right)\)
=> P \(\ge3\)
Dấu "=" xảy ra <=> a = b = c
mà a + b + c = 3
=> a = b = c = 1
Vậy Min P = 3 <=> a = b= c = 1