Cho ΔABC cân tại A, có Bˆ = 40°. Tính Aˆ
Ai giúp mik với !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
1
H9
HT.Phong (9A5)
CTVHS
19 tháng 8 2023
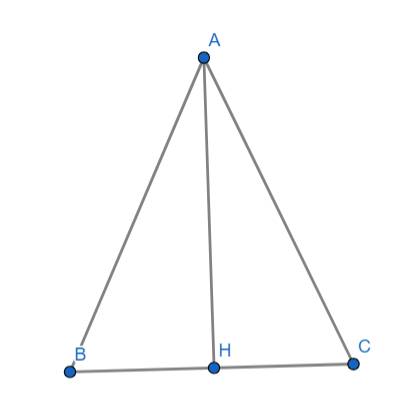
Do tam giác ABC là tam giác cân nên AH là đường cao đồng thời là đường trung tuyến nên:
\(BH=CH=\dfrac{BC}{2}=\dfrac{5}{2}=2,5\left(cm\right)\)
Xét tam giác vuông ABH ta có:
\(sinB=\dfrac{BH}{AB}\)
\(\Rightarrow sin40^{o0}=\dfrac{2,5}{AB}\Rightarrow AB=\dfrac{2,5}{sin40^o}\approx4\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác đó ta có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{4^2-2,5^2}\approx3\left(cm\right)\)
11 tháng 7 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>DH=EH
=>ΔHDE cân tại H
H9
HT.Phong (9A5)
CTVHS
19 tháng 8 2023
1) Mình làm rồi nhé:
https://hoc24.vn/cau-hoi/cho-dabc-can-tai-a-co-bc-5cm-b-c-40-tinh-ab-va-duong-cao-ah.8311486416239
2) Xét tam giác vuông ABH ta có:
\(cosB=\dfrac{AH}{AB}\)
\(\Rightarrow cos60^o=\dfrac{5}{AB}\Rightarrow AB=\dfrac{5}{cos60^o}=10\)
Áp dụng định lý Py-ta-go vào tam giác này ta có:
\(AB^2=AH^2+BH^2\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{10^2-5^2}=5\sqrt{3}\)
Mà: \(BH+CH=BC\)
\(\Rightarrow CH=BC-BH=10-5\sqrt{3}\approx1,3\)
Áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{CH^2+AH^2}=\sqrt{1,3^2+5^2}\approx5,2\)
ND
1
15 tháng 9 2021
\(AB=\sqrt{\dfrac{BC^2}{2}}=\sqrt{\dfrac{9a^2}{2}}=\sqrt{\dfrac{18a^2}{4}}=\dfrac{3a\sqrt{2}}{2}\)
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{18a^2}{4}:2=\dfrac{18a^2}{8}=\dfrac{9a^2}{4}\)
vì tam giác ABC cân tại A
=> góc B = góc C = 40 độ
=> góc A=180 độ - 40 độ - 40 độ =100 độ
k nha
Vì \(\Delta\)ABC cân tại A nên ta có : \(\widehat{B}=\widehat{C}=40^0\)
=> \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{A}=180^0-\left(\widehat{B}+\widehat{C}\right)\)
\(=180^0-80^0\)
\(=100^0\)
Vậy \(\widehat{A}=100^0\)