đkxđ ; x>hoac = 0 , x khac 9 so sanh A=\(\frac{\sqrt{x}}{\sqrt{x}+1}\) va B=\(\frac{\sqrt{x}-2}{\sqrt{x}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
GH
8 tháng 7 2023
Để \(\sqrt{\dfrac{2\sqrt{15}-\sqrt{59}}{x-7}}\) được xác định thì \(\dfrac{2\sqrt{15}-\sqrt{59}}{x-7}\ge0\)
\(\Leftrightarrow x-7>0\\ \Leftrightarrow x>7\)
Để \(\sqrt{\dfrac{-2\sqrt{6}+\sqrt{23}}{-x+5}}\) được xác định thì \(\dfrac{-2\sqrt{6}+\sqrt{23}}{-x+5}\ge0\)
\(\Leftrightarrow-x+5< 0\\ \Leftrightarrow x>5\)
1 tháng 7 2023
Vì các số trong căn bậc `2` không âm nên căn thức được xác định.
KK
6 tháng 9 2021
2TH (mik dự đoán)
TH1: Nếu là \(\sqrt{x}-1\) => ĐKXĐ: x \(\ge\) 0
TH2: Nếu là \(\sqrt{x-1}\) => ĐKXĐ: \(x\ge1\)
12 tháng 1 2023
ĐKXĐ: x<>0; x<>2; x<>1; x<>-1
\(Q=1+\dfrac{x+1+x+1-2x^2+2x-2}{\left(x+1\right)\left(x^2-x+1\right)}\cdot\dfrac{x\left(x^2-x-1\right)}{x^2\left(x-2\right)}\)
\(=1+\dfrac{-2x^2+4x}{\left(x+1\right)}\cdot\dfrac{1}{x\left(x-2\right)}\)
\(=1+\dfrac{-2x\left(x-2\right)}{x\left(x+1\right)\left(x-2\right)}=1+\dfrac{-2}{x+1}=\dfrac{x+1-2}{x+1}=\dfrac{x-1}{x+1}\)
1 tháng 12 2021
\(ĐKXĐ:9-x^2\ge0\Leftrightarrow x^2\le9\Leftrightarrow-3\le x\le3\)
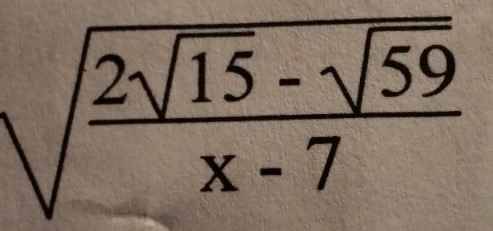
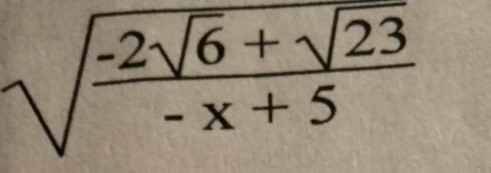
ta có A\(=\frac{\sqrt{x}}{\sqrt{x}+1}=\frac{\sqrt{x}+1}{\sqrt{x}+1}-\frac{1}{\sqrt{x}+1}=1-\frac{1}{\sqrt{x}+1}\)
và B\(=\frac{\sqrt{x}-2}{\sqrt{x}}=\frac{\sqrt{x}}{\sqrt{x}}-\frac{2}{\sqrt{x}}=1-\frac{2}{\sqrt{x}}\)
ta đi so sánh hai số trừ của A và B : \(\frac{1}{\sqrt{x}+1}\)và\(\frac{2}{\sqrt{x}}\)
\(\frac{1}{\sqrt{x}+1}=\frac{2}{2\sqrt{x}+2}\)mà \(2\sqrt{x}+2>\sqrt{x}\)\(\Rightarrow\frac{2}{2\sqrt{x}+2}< \frac{2}{\sqrt{x}}\)
Mà số trừ càng lớn thì phép trừ đó có giá trị bé => A > B