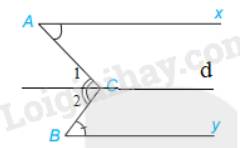
Cho hình vẽ :
Đề bài :
\(\widehat{A1}=\widehat{B1}\), \(\widehat{B2}=35^o\), \(\widehat{BCz}=145^o\)
a) Chứng minh : \(\text{Ax}//By\)
b ) Chứng minh \(m\pm By\)
c ) Chứng minh \(\text{Ax}//Cz\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cửa hàng bán được một tạ rưỡi gẹo tẻ và gạo nếp ; trong đó 25% là gạo nếp. hỏi của hàng bán mỗi loại bao nhiêu ki-lô-gam gạo

Qua C kẻ đường thẳng d song song với Ax
Vì Ax // By nên d // By
Vì d // Ax nên \(\widehat A = \widehat {{C_1}}\)(2 góc so le trong)
Vì d // By nên \(\widehat B = \widehat {{C_2}}\) (2 góc so le trong)
Mà \(\widehat C = \widehat {{C_1}} + \widehat {{C_2}}\)
Vậy \(\widehat C = \widehat A + \widehat B\)(đpcm)

Vì các tia và ở trong góc nên:
(1)
(2)
Từ (1) và (2), suy ra: .
b) Ta có
c) Từ giả thiết, ta có: .
Mà .
Vậy .

Đêm qua em hỏi, chị lại ko nghĩ là em :V
Bài 1:
*Hình ảnh chỉ mang tính chất minh họa
a) Ta có: \(xy\)\(//BD\)
Mà \(BD\)là phân giác \(\widehat{ABC}\) \(\Rightarrow BD\)cắt \(BC\)
\(\Rightarrow xy\)cắt \(BC\) ( gọi giao điểm là M )
b) Ta có: \(\widehat{A_1}=\widehat{B_1}\left(slt\right)\) mà \(\widehat{B_1}=\widehat{B_2}\left(gt\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{B_2}\left(1\right)\)
Mặt khác \(\widehat{M_1}=\widehat{B_2}\left(đvi\right)\left(2\right)\)
Từ \(\left(1\right)\&\left(2\right)\Rightarrow\widehat{A_1}=\widehat{M_1}\)
c) Xét \(\Delta BAM\)có \(\widehat{A_1}=\widehat{M_1}\)(câu b)
\(\Rightarrow\Delta BAM\)cân tại \(B\)
\(\Delta BAM\)cân tại \(B\) có \(BN\) là đường phân giác
=> \(BN\)đồng thời là đường cao của \(\Delta BAM\)
=> Đpcm
Bài 2:
*Hình ảnh chỉ mang tính chất minh họa (Nhinf cais anhr thaays gowms quas)
a) Ta cos: \(AH\) vuông góc \(By\)\(;\) \(CK\)vuông góc \(Bx\)
Mà Bx tạo với tia By một góc 150 độ => Bx cắt By tại B
=> AH cắt CK ( tại giao điểm I )
b) Ta có: \(\widehat{ABC}=150^o\Rightarrow\widehat{ABH}=30^o\)
\(\Rightarrow\widehat{BAH}=90-\widehat{ABH}=60^o\)
\(\Rightarrow\widehat{AIC}=\widehat{AIK}=90-\widehat{BAH}=30^o\)
@@ Cách khác
Ta có: \(\widehat{HBK}=\widehat{ABC}=150^o\left(đđ\right)\)
Xét tứ giác BHIK có:
\(\widehat{AIC}=360-\widehat{IHB}-\widehat{IKB}-\widehat{HBK}\) (Nếu chưa học cái này thì chứng minh bằng cách chia tứ giác thành 2 tam giác)
\(\Leftrightarrow\widehat{AIC}=360-90-90-150=30^o\)
B1 :a)BC ko song song với BD vì chung B
->BC ko sog sog xy (xy//BD) nên cắt BC tại M
b)
c)NBA+ANB+BNA=180^o
NMB+MBN+BNM=180^o
AMB=MAB; B1=B2 (BN pg ABM)
Nen N1=N2;N1+N2=180^o ->ĐPCM
mỏi quá r` mai nghĩ tiếp mà vẽ hộ tui cái hình bài 2 vs

a) Theo đề bài ta có tam giác ABC cân ở A và \(\widehat A = {56^o}\)
Mà \( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat B = \widehat C = ({180^o} - {56^o}):2 = {62^o}\)
b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )
Mà M, N là trung điểm của AB, AC
Nên AM = AN
Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A
\( \Rightarrow \widehat M = \widehat N = ({180^o} - {56^o}):2 = {62^o}\)
c) Vì \(\widehat {AMN}=\widehat {ABC}\) (cùng bằng 62°)
Mà chúng ở vị trí đồng vị nên MN⫽BC

a) Vì \(\Delta ABC\) cân tại \(A\left(gt\right)\)
=> \(\left\{{}\begin{matrix}AB=AC\\\widehat{B}=\widehat{C}\end{matrix}\right.\) (tính chất tam giác cân).
Xét \(\Delta ABC\) có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) (định lí tổng 3 góc trong một tam giác).
=> \(\widehat{B}+\widehat{C}=180^0-\widehat{A}\) (1).
Mà \(\widehat{B}=\widehat{C}\left(cmt\right)\)
=> \(\widehat{B}=\widehat{C}=\frac{\widehat{A}}{2}\) (2).
Từ (1) và (2) => \(\widehat{B}=\widehat{C}=180^0-\frac{\widehat{A}}{2}.\)
b) Xét 2 \(\Delta\) vuông \(AHB\) và \(AHC\) có:
\(\widehat{AHB}=\widehat{AHC}=90^0\left(gt\right)\)
\(AB=AC\left(cmt\right)\)
Cạnh AH chung
=> \(\Delta AHB=\Delta AHC\) (cạnh huyền - cạnh góc vuông).
=> \(HB=HC\) (2 cạnh tương ứng).
=> \(\widehat{BAH}=\widehat{CAH}\) (2 góc tương ứng).
c) Ta có:
\(\left\{{}\begin{matrix}AM+BM=AB\\AN+CN=AC\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}BM=CN\left(gt\right)\\AB=AC\left(cmt\right)\end{matrix}\right.\)
=> \(AM=AN.\)
=> \(\Delta AMN\) cân tại A.
Chúc bạn học tốt!
a) Vì A1 = B1 mà A1 và B1 là 2 góc đồng vị => Ax // By
b) Ta có : Ax ⊥ m ; Ax // By => By ⊥ m
c) Vì B2 = 35o ; BCz = 145o
=> B2 + BCz = 180o mà B2 và BCz là 2 góc trong cùng phía
=> By // Cz mà By // Ax
=> Ax // Cz
cho mk hỏi là hình có vẽ Ax vuông góc với m ko ah?
a, Ta có : \(\widehat{A_1}=\widehat{B_1}\) ( gt ). mà 2 góc này ở vị trí đồng vị của Ax và By => Ax // By ( dhnb ) (1)
b, Ta có : Ax // By (cmt ) ; Ax \(\perp m\) ( cách vẽ ) => By \(\perp m\) ( quan hệ từ vuông góc đến //)
c, Ta có : góc B2 = 35o ( gt ); góc BCz = 145o ( gt )
mà 2 góc này ở vị trí trong cùng phía ( do 35o +145o = 180o ) => By // Cz ( dhnb ) (2)
từ (1) và (2) => Ax// Cz ( // By ) ( đpcm )