Cho \(\Delta\)ABC = \(\Delta\)MNP có \(\widehat{N}\)= 60 độ; \(\widehat{P}\)= 80 độ
Tính các góc \(\Delta\)ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 50^\circ + 60^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 70^\circ \end{array}\)
Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P = 70^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g).

Vì \(\Delta ABC \backsim \Delta MNP\) nên:
\(\left\{ \begin{array}{l}\widehat A = \widehat M = 45^\circ \\\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P\end{array} \right.\)
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\45^\circ + 60^\circ + \widehat C = 180^\circ \\\widehat C = 180^\circ - 45^\circ - 60^\circ = 75^\circ \end{array}\)
\( \Rightarrow \widehat C = \widehat P = 75^\circ \)

Ta có: \(\Delta ABC = \Delta MNP\) nên \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Mà \(\widehat A + \widehat N = 125^\circ \)hay \(\widehat M + \widehat N = 125^\circ \). Tổng ba góc trong một tam giác bằng 180°.
Trong tam giác MNP:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\125^\circ + \widehat P = 180^\circ \\ \to \widehat P = 180^\circ - 125^\circ = 55^\circ \end{array}\)
Vậy số đo góc P là 55°.

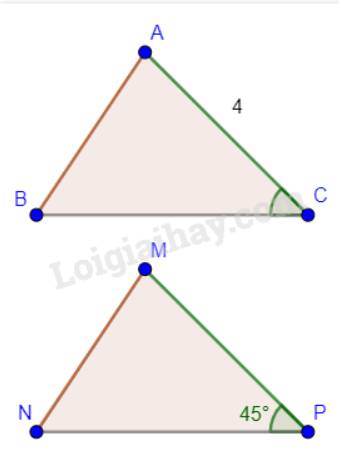
\(\Delta ABC = \Delta MNP\) nên \(AC = MP\)và \(\widehat {MPN} = \widehat {ACB}\).
Vậy \(MP = 4\)cm và \(\widehat {ACB} = 45^\circ \).

a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.

A B C M N P H K
Kẻ \(BH⊥AC;NK⊥MP\)
Khi đó ta thấy ngay \(\Delta MNK\sim\Delta ABH\left(g-g\right)\Rightarrow\frac{NK}{BH}=\frac{MN}{AB}\)
Lại có \(\frac{S_{MNP}}{S_{ABC}}=\frac{\frac{1}{2}.MP.NK}{\frac{1}{2}.AC.BH}=\frac{NK}{BH}.\frac{MP}{AC}=\frac{MN}{AB}.\frac{MP}{AC}=\frac{MN.MP}{AB.AC}\left(đpcm\right)\)
Theo như đề bài ta đã có các góc N và P. Vậy ta cần tính góc M
(-) Như ta biết tổng ba góc của một tam giác bằng 180o
=> N + P + M = 180o
60o + 80o + M = 180o
140 o + M = 180o
M = 180o - 140o
M = 40o
Vì tam giác ABC = tam giác MNP nên góc A = M; B = N; C = P
=> A = 40o; B = 60o; C = 80o
Xin lỗi bạn mik không biết ghi góc như bạn nên mong bạn thông cảm
Học tốt!!!
Ta có:\(\widehat{M}\)+\(\widehat{N}\)+\(\widehat{P}\)=180 độ
Mà \(\widehat{N}\)=60 độ;\(\widehat{P}\)=80 độ suy ra \(\widehat{M}\)=40 độ
Vì\(\Delta ABC=\Delta MNP\)suy ra \(\widehat{A}=\widehat{M}\);\(\widehat{B}=\widehat{N}\);\(\widehat{C}=\widehat{P}\)
\(\Rightarrow\)\(\widehat{A}=40\)độ ;\(\widehat{B}=60\)độ ;\(\widehat{C}=80\)độ