Tìm x thuộc Z để mỗi p/s sau là 1 số TN:
a)x+6x+1
b)x−2x+3
c)2x+1x−3
...
Đọc tiếp
Tìm x thuộc Z để mỗi p/s sau là 1 số TN:
a)x+6x+1
b)x−2x+3
c)2x+1x−3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 8 2018
a) ta có: \(\frac{x+6}{x+1}=\frac{x+1+5}{x+1}=1+\frac{5}{x+1}\)
Để \(\frac{x+6}{x+1}\in Z\)
=> 5/x+1 thuộc Z
=> 5 chia hết cho x + 1
=> x + 1 thuộc Ư(5)={1;-1;5;-5}
...
rùi bn tự lập bảng xét giá trị hộ mk nha! câu b lm tương tự
c) ta có: \(\frac{2x+1}{x-3}=\frac{2x-6+7}{x-3}=\frac{2.\left(x-3\right)+7}{x-3}=2+\frac{7}{x-3}\)
...
U
9 tháng 8 2018
\(a,\frac{x+6}{x+1}\inℤ\Leftrightarrow x+6⋮x+1\)
\(\Rightarrow x+1+5⋮x+1\)
\(x+1⋮x+1\)
\(\Rightarrow5⋮x+1\)
\(\Rightarrow x+1\inƯ\left(5\right)\)
\(\Rightarrow x+1\in\left\{-1;1;-5;5\right\}\)
\(\Rightarrow x\in\left\{-2;0;-6;4\right\}\)
vậy_
\(c,\frac{2x+1}{x-3}\inℤ\Leftrightarrow2x+1⋮x-3\)
\(\Rightarrow2x-6+7⋮x-3\)
\(\Rightarrow2\left(x-3\right)+7⋮x-3\)
\(2\left(x-3\right)⋮x-3\)
\(\Rightarrow7⋮x-3\)
\(\Rightarrow x-3\inƯ\left(7\right)\)
\(\Rightarrow x-3\in\left\{-1;1;-7;7\right\}\)
\(\Rightarrow x\in\left\{2;4;-4;10\right\}\)
vậy_
phần b thì làm tương tự phần a
T
0
18 tháng 11 2017
MK ko biế đúng ko nữa , sai thì ý kiến
a)
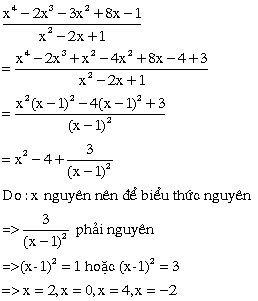
b)
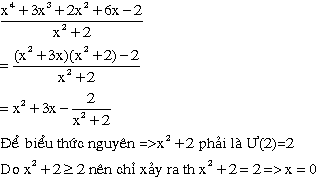
Chúc các bn hok tốt
Tham khảo nhé
CH
Cô Hoàng Huyền
Admin
VIP
21 tháng 8 2017
a) Giả sử \(C=\frac{2x+3}{7}=t\left(t\in Z\right)\)
\(\Rightarrow x=\frac{7t-3}{2}\). Để \(x\in Z\) thì t phải lẻ. Nói cách khác \(t=2k+1\left(k\in Z\right)\)
Suy ra \(x=\frac{7\left(2k+1\right)-3}{2}=14k+2\)
Vậy để \(\frac{2x+3}{7}\in Z\) thì \(x=14k+2\left(k\in Z\right)\)
b) Ta thấy \(C=\frac{6x-1}{3x+2}=\frac{\left(6x+4\right)-5}{3x+2}=2-\frac{5}{3x+2}\)
Do x nguyên nên C đạt GTNN khi \(\frac{5}{3x+2}\) lớn nhất. Điều này xảy ra khi 3x + 2 = 2 hay x = 0.
Vậy \(minC=-\frac{1}{2}\) khi x = 0.
T
4
6 tháng 5 2015
để A là số nguyên thì 2x+1 chia hết cho x-3
ta có:2x+1 chia hết cho x-3
2x-6+7 chia hết cho x-3
2x-2.3+7 chia hết cho x-3
2 (x-3)+7 chia hết cho x-3
2 (x-3) chia hết cho x-3 thì 7 chia hết cho x-3
x-3 thuộc ước của 7. đến đây thì bạn tự làm đc r.
Để đây là số tự nhiên thì \(\left\{{}\begin{matrix}x+3-5⋮x+3\\\dfrac{x-2}{x+3}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+3\in\left\{1;-1;5;-5\right\}\\\left[{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x\in\left\{-4;-8\right\}\)