Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


vi UCLN(a,b)=57
\(\Rightarrow a⋮57,b⋮57\)
\(\Rightarrow a=57m\)va \(b=57n\)
ma a+b=228\(\Rightarrow56m+56n=228\)
=>m+n=4
Vay: Ta co bang:
| m | 1 | 2 | 3 |
| n | 3 | 2 | 1 |
Vay:\(\hept{\begin{cases}a=1.57=57\\b=3.57=171\end{cases}}\)hoac\(\hept{\begin{cases}a=2.57=114\\b=2.57=114\end{cases}}\)hoac\(\hept{\begin{cases}a=3.57=171\\b=1.57=57\end{cases}}\)


1)vì ƯCLN(a,b)=64,giả sử a>b
\(\hept{\begin{cases}a=64m\\b=64n\end{cases}}\left(m,n\right)=1,m>n\)
ta có a+b=256
=>64m+64n=256
=> 64(m+n)=256
m+n=4
| a | 192 | |
| m | 3 | |
| n | 1 | |
| b | 64 |
vậy (a,b) là (192,64),(64,192)
câu b tương tự
có khác 1 tí là
=>48mx48n=13824
=>2304mxn=13824

ta gọi d là ước chung lớn nhất của a và b và = 19
a =19 n
b = 19m ( m;n) = 1
a + b = 19n + 19m = 19. ( n + m ) = 228
\(\Rightarrow\)n + m = 228 : 19 = 12
(1;11 ) ; ( 5;7)
Ta thử n =1 và m =11
a = 19.1 = 19
b = 19.11= 209
mà 209 + 19 = 228 và ƯCLN ( 19 ; 209 ) = 19 ( chọn )
Ta thử n =5; m =7
a = 95
b = 133
có UCLN là 19 ( chọn )
Vậy có 2 cặp a ;b thỏa mãn
Đặt a=19m(m thuộc N sao)
B=19n(n thuộc N sao)
=>BCNN(a,b)=19mn
vì ƯCLN(a,b)=19=>ƯCLN(m,n)=1
Giả sử a<b=>m<n
ta có ;a+b=228
=>19m+19n=228
=>19.(m+n)=228
=>m+n=12
=>m thuộc {1,2,3,4,5}
Nếu m=1=>n=11
=>a=19=>b=209
......
có lập bảng giá trị


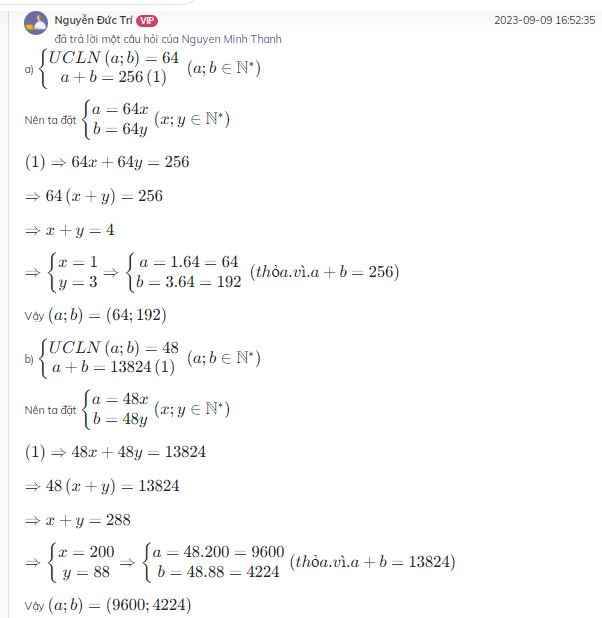
a) \(\left\{{}\begin{matrix}UCLN\left(a;b\right)=64\\a+b=256\left(1\right)\end{matrix}\right.\) \(\left(a;b\inℕ^∗\right)\)
Nên ta đặt \(\left\{{}\begin{matrix}a=64x\\b=64y\end{matrix}\right.\) \(\left(x;y\inℕ^∗\right)\)
\(\left(1\right)\Rightarrow64x+64y=256\)
\(\Rightarrow64\left(x+y\right)=256\)
\(\Rightarrow x+y=4\)
\(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1.64=64\\b=3.64=192\end{matrix}\right.\) \(\left(thỏa.vì.a+b=256\right)\)
Vậy \(\left(a;b\right)=\left(64;192\right)\)
b) \(\left\{{}\begin{matrix}UCLN\left(a;b\right)=48\\a+b=13824\left(1\right)\end{matrix}\right.\) \(\left(a;b\inℕ^∗\right)\)
Nên ta đặt \(\left\{{}\begin{matrix}a=48x\\b=48y\end{matrix}\right.\) \(\left(x;y\inℕ^∗\right)\)
\(\left(1\right)\Rightarrow48x+48y=13824\)
\(\Rightarrow48\left(x+y\right)=13824\)
\(\Rightarrow x+y=288\)
\(\Rightarrow\left\{{}\begin{matrix}x=200\\y=88\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=48.200=9600\\b=48.88=4224\end{matrix}\right.\) \(\left(thỏa.vì.a+b=13824\right)\)
Vậy \(\left(a;b\right)=\left(9600;4224\right)\)
b,Theo bài ra ta có:
a + b =13824
ƯCLN (a,b)=48
*Vì ƯCLN (a,b) =48 => a=48x (x < y, ƯCLN (x,y ) = 1)
b=48y
*Mà a + b = 13824
=> 48x + 48y = 13824
48(x + y) = 13824 : 48
x + y = 288
*Ta phải tìm hai số x,y thỏa mãn các điều kiện :
x < y
UCLN (x,y) = 1
x + y =4
=>Với x=1 thì y=3
Lập bảng:
x=1
y=3
a=288 . 1 = 288 thuộc N
b=288 . 3 = 864 thuộc N
Vậy a=288,b=864.
a,Theo bài ra ta có:
a + b =256
ƯCLN (a,b)=64
*Vì ƯCLN (a,b) =64 => a=64x (x < y, ƯCLN (x,y ) = 1)
b=64y
*Mà a + b = 256
=> 64x + 64y = 256
64(x + y) = 256 : 64
x + y = 4
*Ta phải tìm hai số x,y thỏa mãn các điều kiện :
x < y
UCLN (x,y) = 1
x + y =4
=>Với x=1 thì y=3
Lập bảng:
x=1
y=3
a=18 . 1 = 18 thuộc N
b=18 . 3 = 54 thuộc N
Vậy a=18,b=54.
Do ƯCLN(a;b) = 57
\(\Rightarrow\)\(\begin{cases} a = 57x\\ b=57y \end{cases}\) (x,y \(\in\) N*)
\(\Rightarrow\) a+b = 57x + 57y = 57(x+y) = 228
\(\Rightarrow\) x+y = 228/7 = 4
Mà x; y \(\in\) N* \(\Rightarrow\) (x; y) \(\in\) {(1; 3);(2; 2);(3; 1)}
\(\Rightarrow\) (a; b) \(\in\) {(57; 171);(114; 114);(171; 57)}
Vậy.....................................