Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)vì ƯCLN(a,b)=64,giả sử a>b
\(\hept{\begin{cases}a=64m\\b=64n\end{cases}}\left(m,n\right)=1,m>n\)
ta có a+b=256
=>64m+64n=256
=> 64(m+n)=256
m+n=4
| a | 192 | |
| m | 3 | |
| n | 1 | |
| b | 64 |
vậy (a,b) là (192,64),(64,192)
câu b tương tự
có khác 1 tí là
=>48mx48n=13824
=>2304mxn=13824

Vì BCNN (a,b) = 300 và ƯCLN (a,b) = 15
=> a.b = 300 .15 = 4500
Vì ƯCLN (a,b) = 15 nên => a = 15m và b = 15n [ với ƯCLNH ( m;n ) = 1 ]
và a+15 = b nên => 15m + 15 = 15n => 15( m+1 ) = 15n => m+1 = n
Mà a.b = 4500 nên ta có :
+) 15m.15n = 4500
+) 15.15.m.n = 4500
+) 152..m.n = 4500
+) 225.m.n = 4500
=> m.n = 20
=> m = 1 và n = 20 hoặc m = 4 và n = 5
mà m+1 = n => m = 4 và n = 5
=> a = 15 . 4 = 60
b = 15 . 5 = 75
Vậy a = 60 và b = 75
Chúc bn hc tốt ! ^^
hình như thiếu đề thì pải
Tìm a,b \(\in\) N, biết:
BCNN (a,b) = 300
ƯCLN (a,b) = 15
và a + 15 = b chứ


Lời giải:
a. Gọi $d=ƯCLN(a,b)$. Khi đó, đặt $a=dx, b=dy$ với $x,y$ là số tự nhiên, $x,y$ nguyên tố cùng nhau.
Khi đó: $BCNN(a,b)=dxy$
Theo bài ra: $d+dxy=19$
$\Rightarrow d(1+xy)=19$
Do $d, 1+xy$ đều là số tự nhiên nên có 2 TH xảy ra:
TH1: $d=1, 1+xy=19\Rightarrow d=1, xy=18$
Do $ƯCLN(x,y)=1$ nên $(x,y)=(1,18), (2,9), (9,2), (18,1)$
$\Rightarrow (a,b)=(dx, dy) +(1,18), (2,9), (9,2), (18,1)$
b,c bạn làm tương tự theo hướng của câu a nhé.


a) Dễ thấy P = 102120 + 2120
= 102120 + 212.10
= 10(102119 + 212)
=> P \(⋮10\)
Lại có P = 102120 + 2120
= 10(102119 + 212)
= 10.(1000...00 + 212)
2119 số 0
= 10.1000...0212
2116 số 0
Tổng các chữ số của số S = 1000...0212 (2116 chữ số 0)
là 1 + 0 + 0 + 0 +.... + 0 + 2 + 1 + 2 (2116 hạng tử 0)
= 1 + 2 + 1 + 2 = 6 \(⋮3\)
=> S \(⋮3\Rightarrow P=10S⋮3\)
mà \(\left\{{}\begin{matrix}P⋮10\\P⋮3\\\left(10,3\right)=1\end{matrix}\right.\Rightarrow P⋮10.3\Rightarrow P⋮30\)
Gọi (a,b) = d \(\left(d\inℕ^∗;d\ne1\right)\)
=> \(\left\{{}\begin{matrix}a⋮d\\b⋮d\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2n+3⋮d\\5n+2⋮d\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}5.(2n+3)⋮d\\2.(5n+2)⋮d\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}10n+15⋮d\left(1\right)\\10n+4⋮d\left(2\right)\end{matrix}\right.\)
Lấy (1) trừ (2) ta được
(10n + 15) - (10n + 4) \(⋮d\)
<=> 11 \(⋮d\)
\(\Leftrightarrow d\in\left\{1;11\right\}\) mà d \(\ne1\)
<=> d = 11
Vậy (a;b) = 11
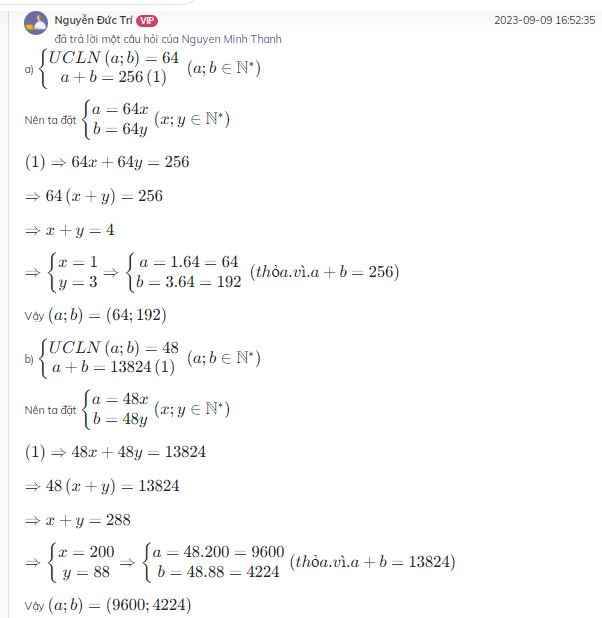

a) \(\left\{{}\begin{matrix}UCLN\left(a;b\right)=64\\a+b=256\left(1\right)\end{matrix}\right.\) \(\left(a;b\inℕ^∗\right)\)
Nên ta đặt \(\left\{{}\begin{matrix}a=64x\\b=64y\end{matrix}\right.\) \(\left(x;y\inℕ^∗\right)\)
\(\left(1\right)\Rightarrow64x+64y=256\)
\(\Rightarrow64\left(x+y\right)=256\)
\(\Rightarrow x+y=4\)
\(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1.64=64\\b=3.64=192\end{matrix}\right.\) \(\left(thỏa.vì.a+b=256\right)\)
Vậy \(\left(a;b\right)=\left(64;192\right)\)
b) \(\left\{{}\begin{matrix}UCLN\left(a;b\right)=48\\a+b=13824\left(1\right)\end{matrix}\right.\) \(\left(a;b\inℕ^∗\right)\)
Nên ta đặt \(\left\{{}\begin{matrix}a=48x\\b=48y\end{matrix}\right.\) \(\left(x;y\inℕ^∗\right)\)
\(\left(1\right)\Rightarrow48x+48y=13824\)
\(\Rightarrow48\left(x+y\right)=13824\)
\(\Rightarrow x+y=288\)
\(\Rightarrow\left\{{}\begin{matrix}x=200\\y=88\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=48.200=9600\\b=48.88=4224\end{matrix}\right.\) \(\left(thỏa.vì.a+b=13824\right)\)
Vậy \(\left(a;b\right)=\left(9600;4224\right)\)
b,Theo bài ra ta có:
a + b =13824
ƯCLN (a,b)=48
*Vì ƯCLN (a,b) =48 => a=48x (x < y, ƯCLN (x,y ) = 1)
b=48y
*Mà a + b = 13824
=> 48x + 48y = 13824
48(x + y) = 13824 : 48
x + y = 288
*Ta phải tìm hai số x,y thỏa mãn các điều kiện :
x < y
UCLN (x,y) = 1
x + y =4
=>Với x=1 thì y=3
Lập bảng:
x=1
y=3
a=288 . 1 = 288 thuộc N
b=288 . 3 = 864 thuộc N
Vậy a=288,b=864.
a,Theo bài ra ta có:
a + b =256
ƯCLN (a,b)=64
*Vì ƯCLN (a,b) =64 => a=64x (x < y, ƯCLN (x,y ) = 1)
b=64y
*Mà a + b = 256
=> 64x + 64y = 256
64(x + y) = 256 : 64
x + y = 4
*Ta phải tìm hai số x,y thỏa mãn các điều kiện :
x < y
UCLN (x,y) = 1
x + y =4
=>Với x=1 thì y=3
Lập bảng:
x=1
y=3
a=18 . 1 = 18 thuộc N
b=18 . 3 = 54 thuộc N
Vậy a=18,b=54.