Tìm chỗ sai trong bài làm sau đây của một học sinh (h.52) :
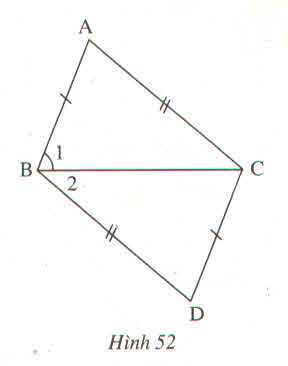
\(\Delta ABC=\Delta DCB\left(c.c.c\right)\Rightarrow\widehat{B}_1=\widehat{B}_2\) (cặp góc tương ứng ) \(\Rightarrow BC\) là tia phân giác của góc ABD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 8 2017
Bạn học sinh suy luận ΔABC = ΔDCB
⇒ ∠(B1) = ∠(B2) là sai vì ∠(B1 ) và ∠(B2 ) không phải là 2 góc tương ứng của hai tam giác bằng nhau nói trên. Do đó không suy luận ra được BC là tia phân giác của góc ABD
23 tháng 11 2017
Tìm chỗ sai trong bài làm sau đây của một học sinh (h.52) :
\(\Delta ABC=\Delta DCB\left(c-c-c\right)\Rightarrow B_2=B_3\)(cặp góc tương ứng) \(\Rightarrow BC\) là tia phân giác của góc ABD
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Ta có: \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\end{array} \right.\).
b) Xét tam giác \(DEF\) có:
\(\widehat D + \widehat E + \widehat F = 180^\circ \) (tổng ba góc trong một tam giác).
Ta có: \(\widehat D = 78^\circ ;\widehat E = 57^\circ \) thay số ta được
\(78^\circ + 57^\circ + \widehat F = 180^\circ \Rightarrow \widehat F = 180^\circ - 78^\circ - 57^\circ = 45^\circ \)
Ta có: \(\Delta DEF\backsim\Delta D'E'F' \Rightarrow \widehat D = \widehat {D'};\widehat E = \widehat {E'};\widehat F = \widehat {F'}\) (các góc tương ứng bằng nhau)
Do đó, \(\widehat D = \widehat {D'} = 78^\circ ;\widehat F = \widehat {F'} = 45^\circ \).
c) Ta có \(\Delta MNP\backsim\Delta M'N'P' \Rightarrow \frac{{MN}}{{M'N'}} = \frac{{MP}}{{M'P'}} = \frac{{NP}}{{N'P'}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Với \(MP = 10;NP = 6;M'N' = 15;N'P' = 12\) thay vào ta được:
\( \Rightarrow \left\{ \begin{array}{l}\frac{{MN}}{{15}} = \frac{1}{2}\\\frac{{10}}{{M'P'}} = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}MN = \frac{{15.1}}{2} = 7,5\\M'P' = \frac{{10.2}}{1} = 20\end{array} \right.\).
Vậy \(MN = 7,5;M'P' = 20\).
TD
21 tháng 10 2016
1 a,Ta có ∆ ABC= ∆ HIK, nên cạnh tương ứng với BC là cạnh IK
góc tương ứng với góc H là góc A.
ta có : ∆ ABC= ∆ HIK
Suy ra: AB=HI, AC=HK, BC=IK.
=
,
=
,
=
.
b,
∆ ABC= ∆HIK
Suy ra: AB=HI=2cm, BC=IK=6cm, =
=400
2.
Ta có ∆ABC= ∆ DEF
Suy ra: AB=DE=4cm, BC=EF=6cm, DF=AC=5cm.
Chu vi của tam giác ABC bằng: AB+BC+AC= 4+5+6=15 (cm)
Chu vi của tam giác DEF bằng: DE+EF+DF= 4+5+6=15 (cm
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}} = \left( {1;3} \right),\overrightarrow {{n_2}} = \left( {1; - 2} \right)\)
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {1.1 + 3.( - 2)} \right|}}{{\sqrt {{1^2} + {3^2}} \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} }} \approx 0,93 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) \approx 22^\circ 8'\)
b) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}} = \left( {4; - 2} \right),\overrightarrow {{n_2}} = \left( {2; - 1} \right)\)
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {4.2 + ( - 2).( - 1)} \right|}}{{\sqrt {{4^2} + {{\left( { - 2} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = 1 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) = 0^\circ \)
c) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}} = \left( {2; - 1} \right),\overrightarrow {{n_2}} = \left( {1;2} \right)\)
Ta có \({a_1}{a_2} + {b_1}{b_2} = 2.1 + ( - 1).2 = 0\)
Suy ra \(\left( {{\Delta _1},{\Delta _2}} \right) = 90^\circ \)
sai ở chỗ góc B1=B2