Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

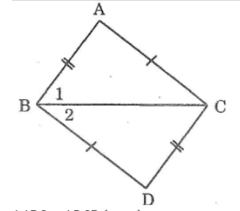
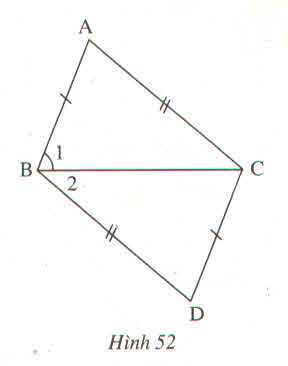
Bạn học sinh suy luận ΔABC = ΔDCB
⇒ ∠(B1) = ∠(B2) là sai vì ∠(B1 ) và ∠(B2 ) không phải là 2 góc tương ứng của hai tam giác bằng nhau nói trên. Do đó không suy luận ra được BC là tia phân giác của góc ABD

a) Xét ΔABH vuông tại H và ΔDBH vuông tại H có
BH chung
HA=HD(gt)
Do đó: ΔABH=ΔDBH(hai cạnh góc vuông)
Suy ra: \(\widehat{ABH}=\widehat{DBH}\)(hai góc tương ứng)
mà tia BH nằm giữa hai tia BA,BD
nên BH là tia phân giác của \(\widehat{ABD}\)(đpcm)
b) Xét ΔACH vuông tại H và ΔDCH vuông tại H có
CH chung
AH=DH(gt)
Do đó: ΔACH=ΔDCH(hai cạnh góc vuông)
Suy ra: CA=CD(hai cạnh tương ứng)
Ta có: ΔABH=ΔDBH(cmt)
nên BA=BD(hai cạnh tương ứng)
Xét ΔABC và ΔDBC có
BA=BD(cmt)
BC chung
CA=CD(cmt)
Do đó: ΔABC=ΔDBC(c-c-c)

Bạn tham khảo link này:
https://olm.vn/hoi-dap/detail/69837898106.html

có 3 cách
cách 1

cách 2

cách 3
a) vì A trung điểm DH
E trung điểm HC
=>F là trọng tâm tam giác DHC
=>HF cắt CD tại TĐ K của CD
b) vì F là trọng tâm tam giác HDC nên HF/HK=1/3
mà HK=1/2CD (do tam giác DHC vuông có HK là trung tuyến)
=>HF=1/3 CD

k nha

-Bạn cho mình hình và lời giải chi tiết được không?
Tìm chỗ sai trong bài làm sau đây của một học sinh (h.52) :
\(\Delta ABC=\Delta DCB\left(c-c-c\right)\Rightarrow B_2=B_3\)(cặp góc tương ứng) \(\Rightarrow BC\) là tia phân giác của góc ABD