Tính tổng hữu hạn : 2.6.8.10+4.6.8.10+6.8.10.12+...+100.102.104.106
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{2.3.4.5+4.6.8.10+6.9.12.15}{2.3.4.5+6.8.10.12+9.12.15.18}\)
= \(\frac{2.3.4.5+2.3.4.5.16+2.3.4.5.81}{2.3.4.5+2.3.4.5.48+2.3.4.5.243}\)
= \(\frac{2.3.4.5.\left(1+16+81\right)}{2.3.4.5.\left(1+48+243\right)}\)
= \(\frac{98}{292}\)
= 49/146
=2.3.4.5+4.6.8.10+6.9.15/2.3.4.5+6.8.10.3.4+9.12.15.6.3
=2.3.4.5+4.6.8.10+6.9.15/3.(2.3.4.5+9.12.15.6)
=1/3
chúc bạn học tốt !

\(A=\dfrac{2.3.4.5+4.6.8.10+6.9.12.15}{2.3.4.5+6.8.10.12+9.12.15.18}\)
\(A=\dfrac{2.3.4.5+2.2.2.3.2.4.2.5.+3.2.3.3.3.4.3.5}{2.3.4.5+2.2.2.3.2.4.2.5+3.3.3.4.3.5.3.6}\)
\(A=\dfrac{2.3.4.5+2^4.2.3.4.5.+3^4.2.3.4.5}{2.3.4.5+2^4.2.3.4.5+3^4.3.4.5.6}\)
\(A=\dfrac{\left(1+2^4+3^4\right)2.3.4.5}{\left(2+2^5+3^4.6\right)3.4.5}\)
\(A=\dfrac{\left(1+2^4+3^4\right)2}{\left(1+2^4+3^5\right).2}\)
\(A=\dfrac{1+2^4+3^4}{1+2^4+3^5}=\dfrac{1+16+81}{1+16+243}=\dfrac{49}{130}\)
\(\dfrac{2.3.4.5+4.6.8.10+6.9.12.15}{2.3.4.5+6.8.10.12+9.12.15.18}\)
\(=\dfrac{4.6.8.10+6.9.12.15}{6.8.10.12+9.12.15.18}\)
\(=\dfrac{1}{3}\)
Kết quả là \(\dfrac{1}{3}\)vì: \(6.8.10.12:4.6.8.10=12:4=3\)
\(9.12.15.18:6.9.12.15=18:6=3\)
Khi cộng vào thì thương không thay đổi và bằng \(\dfrac{1}{3}\)

Chọn C.
- Ta có:
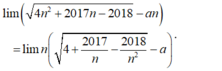
- Vì:
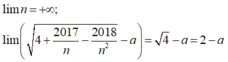
- Suy ra:  có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.
có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.

Chọn C.
- Ta có:
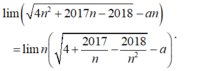
- Vì:
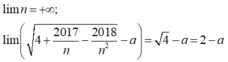
- Suy ra:  có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.
có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.

Tổng là:
[(2018 - 8) : 2 + 1] x (2018 + 8) : 2 + [(2022 - 2020) : 1 + 1] x (2022 + 2020) : 2 = 1019078 + 6063 = 1025141
Đ/S : 1025141

Dãy ( u n + v n ) không có giới hạn hữu hạn.
Thật vậy, giả sử ngược lại ( u n + v n ) có giới hạn hữu hạn.
Khi đó, các dãy số ( u n + v n ) v à ( u n ) cùng có giới hạn hữu hạn, nên hiệu của chúng cũng là một dãy có giới hạn hữu hạn, nghĩa là dãy số có số hạng tổng quát là u n + v n − u n = v n có giới hạn hữu hạn. Điều này trái với giả thiết ( v n ) không có giới hạn hữu hạn.

\(u_n:\left\{{}\begin{matrix}u_1=0;u_1=1\\u_{n+2}=\dfrac{u_{n+1}}{u_{n+1}+u_{n+2}}\end{matrix}\right.\)
Giả sử \(limu_n=a\Rightarrow limu_{n+1}=limu_{n+2}=a\)
\(\Rightarrow a=\dfrac{a}{a+a}=\dfrac{a}{2a}=\dfrac{1}{2}\)
Nên dãy \(u_n\) có giới hạn hữu hạn
vì \(\left\{{}\begin{matrix}u_1=0\\u_2=1>0\end{matrix}\right.\)
\(\Rightarrow u_{n+2}=\dfrac{u_{n+1}}{u_{n+1}+u_{n+2}}>0,\forall n\inℕ\)
\(\Rightarrow a>0\)
\(\Rightarrow limu_n=a=\dfrac{1}{2}\)
Đặt tổng trên là A có:
A = 2.4.6.8 +..+ 100.102.104.106
10A = 2.4.6.8.(10- 0) + 4.6.8.10.(12-2) +....+100.102.104.106.(108-98)
10A= 2.4.6.8.10 + 4.6.8.10.12 -2.4.6.8.10 +....+ 100.102.104.106.108 -98.100.102.104.106
10A= 100.102.104.106.108