Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
- Ta có:
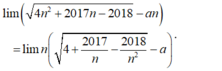
- Vì:
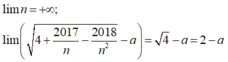
- Suy ra:  có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.
có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.

\(lim\left(\frac{3n+2}{n+2}+a^2-4a\right)=lim\left(\frac{3+\frac{2}{n}}{1+\frac{2}{n}}+a^2-4a\right)=a^2-4a+3\)
\(\Rightarrow a^2-4a+3=0\Rightarrow\left[{}\begin{matrix}a=1\\a=3\end{matrix}\right.\)
\(\Rightarrow S=4\)

Hàm số xác định trên R khi và chỉ khi:
\(2cos^2x-m.sinx+1>0\) ;\(\forall x\)
\(\Leftrightarrow2-2sin^2x-m.sinx+1>0\) ;\(\forall x\)
\(\Leftrightarrow-2sin^2x-m.sinx+3>0\)
Đặt \(sinx=t\Rightarrow f\left(t\right)=-2t^2-m.t+3>0\) ; \(\forall t\in\left[-1;1\right]\)
\(\Leftrightarrow\min\limits_{\left[-1;1\right]}f\left(t\right)>0\)
Do \(a=-2< 0\Rightarrow f\left(t\right)_{min}\) luôn rơi vào 1 trong 2 đầu mút của đoạn
\(f\left(-1\right)=m+1\) ; \(f\left(1\right)=1-m\)
TH1: \(f\left(t\right)_{min}=m+1\Rightarrow\left\{{}\begin{matrix}m+1>0\\1-m\ge m+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-1\\m\le0\end{matrix}\right.\) \(\Leftrightarrow-1< m\le0\)
TH2: \(f\left(t\right)_{min}=1-m\Rightarrow\left\{{}\begin{matrix}1-m>0\\m+1\ge1-m\end{matrix}\right.\) \(\Rightarrow0\le m< 1\)
Vậy \(-1< m< 1\)
Có duy nhất 1 giá trị nguyên của m thỏa mãn (m=0)

1.
Hàm tuần hoàn với chu kì \(2\pi\) nên ta chỉ cần xét trên đoạn \(\left[0;2\pi\right]\)
\(y'=\frac{-4}{\left(cosx-2\right)^2}.sinx=0\Leftrightarrow x=k\pi\)
\(\Rightarrow x=\left\{0;\pi;2\pi\right\}\)
\(y\left(0\right)=-3\) ; \(y\left(\pi\right)=\frac{1}{3}\) ; \(y\left(2\pi\right)=-3\)
\(\Rightarrow\left\{{}\begin{matrix}M=\frac{1}{3}\\m=-3\end{matrix}\right.\)
\(\Rightarrow9M+m=0\)
2.
\(\Leftrightarrow y.cosx+y.sinx+2y=2k.cosx+k+1\)
\(\Leftrightarrow y.sinx+\left(y-2k\right)cosx=k+1-2y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\Rightarrow y^2+\left(y-2k\right)^2\ge\left(k+1-2y\right)^2\)
\(\Leftrightarrow2y^2-4k.y+4k^2\ge4y^2-4\left(k+1\right)y+\left(k+1\right)^2\)
\(\Leftrightarrow2y^2-4y-3k^2+2k+1\le0\)
\(\Leftrightarrow2\left(y-1\right)^2\le3k^2-2k+1\)
\(\Leftrightarrow y\le\sqrt{\frac{3k^2-2k+1}{2}}+1\)
\(y_{max}=f\left(k\right)=\frac{1}{\sqrt{2}}\sqrt{3k^2-2k+1}+1\)
\(f\left(k\right)=\frac{1}{\sqrt{2}}\sqrt{3\left(k-\frac{1}{3}\right)^2+\frac{2}{3}}+1\ge\frac{1}{\sqrt{3}}+1\)
Dấu "=" xảy ra khi và chỉ khi \(k=\frac{1}{3}\)
Đáp án A

Lời giải:
\(\lim\limits _{x\to 0}\frac{(x+a)^3-a^3}{x}=\lim\limits _{x\to 0}\frac{x[(x+a)^2+a(x+a)+a^2]}{x}=\lim\limits _{x\to 0}[(x+a)^2+a(x+a)+a^2]\)
\(=3a^2\)
Để \(\lim\limits _{x\to 0}\frac{(x+a)^3-a^3}{x}=a\) \(\Leftrightarrow 3a^2=a\)
\(\Leftrightarrow 3a^2-a=0\Leftrightarrow a=0; a=\frac{1}{3}\) (có 2 giá trị thực của a)
Đáp án A.
Chọn C.
- Ta có:
- Vì:
- Suy ra: có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.
có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.