tính số đo các góc của tứ giác ABCD biết: \(\dfrac{< A-1^o}{4}\)=\(\dfrac{< B-2^o}{3}\)=\(\dfrac{< C-3^o}{2}\)=\(\dfrac{< D-4^o}{1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 7 2022
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a-1}{4}=\dfrac{b-2}{3}=\dfrac{c-3}{2}=\dfrac{d-4}{1}=\dfrac{a+b+c+d-1-2-3-4}{4+3+2+1}=\dfrac{350}{10}=35\)
Do đó: a-1=140; b-2=105; c-3=70; d-4=35
=>a=141; b=107; c=73; d=39
15 tháng 7 2023
\(\dfrac{A}{1}=\dfrac{B}{2}=\dfrac{C}{3}=\dfrac{D}{4}=\dfrac{A+B+C+D}{1+2+3+4}=\dfrac{360}{10}=36\)
\(\Rightarrow A=36^0;B=36.2=72^0;C=36.3=108^0;D=36.4=144^0\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2022
Do tứ giác ABCD nội tiếp \(\Rightarrow B+D=180^0\) (1)
Mà \(\dfrac{B}{D}=\dfrac{2}{3}\Rightarrow B=\dfrac{2}{3}D\)
Thế vào (1):
\(\dfrac{2}{3}D+D=180^0\Rightarrow\dfrac{5}{3}D=180^0\)
\(\Rightarrow D=108^0\)
\(B=\dfrac{2}{3}D=\dfrac{2}{3}.108^0=72^0\)
16 tháng 6 2023
a: Sửa đề: sin x=4/5
cosx=-3/5; tan x=-4/3; cot x=-3/4
b: 270 độ<x<360 độ
=>cosx>0
=>cosx=1/2
tan x=căn 3; cot x=1/căn 3
23 tháng 7 2022
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a-1}{4}=\dfrac{b-2}{3}=\dfrac{c-3}{2}=\dfrac{d-4}{1}=\dfrac{a+b+c+d-1-2-3-4}{4+3+2+1}=\dfrac{360-10}{10}=35\)
Do đó: a-1=140; b-2=105; c-3=70; d-4=35
=>a=141; b=107; c=73; d=39
AH
Akai Haruma
Giáo viên
4 tháng 5 2023
Lời giải:
$\widehat{AOB}=2\widehat{ACB}=2.45^0=90^0$
Tam giác $OAB$ vuông cân tại $O$ nên $OA=\frac{AB}{\sqrt{2}}=\frac{a}{\sqrt{2}}$
Chu vi hình tròn $(O)$:
$2\pi OA=a\sqrt{2}\pi$
Độ dài cung nhỏ AB: $a\sqrt{2}\pi.\frac{90^0}{360^0}=\frac{a\sqrt{2}\pi}{4}$
Đáp án B.
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
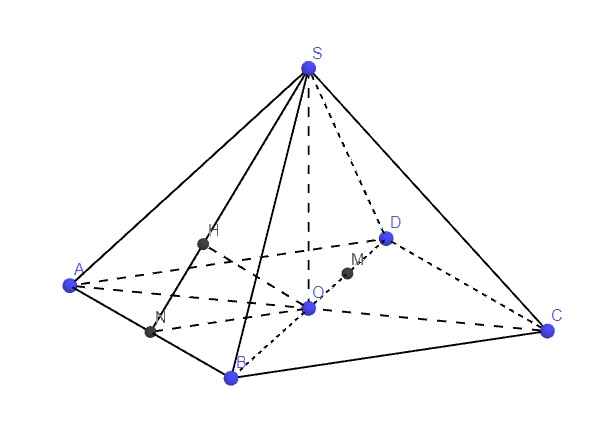
Gọi N là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}ON\perp AB\\SO\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SON\right)\)
Từ O kẻ \(OH\perp SN\) (H thuộc SN) \(\Rightarrow OH\perp\left(SAB\right)\Rightarrow OH=d\left(O;\left(SAB\right)\right)\)
\(ON=\dfrac{1}{2}AD=\dfrac{a}{2}\) ; \(SO=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(OH=\dfrac{SO.ON}{\sqrt{SO^2+ON^2}}=\dfrac{a\sqrt{6}}{6}\)
Lại có: M là trung điểm OD \(\Rightarrow OM=\dfrac{1}{2}OD\Rightarrow BM=\dfrac{3}{2}OB\)
\(\Rightarrow d\left(M;\left(SAB\right)\right)=\dfrac{3}{2}d\left(O;\left(SAB\right)\right)=\dfrac{3}{2}.\dfrac{a\sqrt{6}}{6}=\dfrac{a\sqrt{6}}{4}\)
