tính hệ số góc của các đường thẳng sau
f(x)=-3x+2:y=4x+17;f(x)=\(\dfrac{17}{18}x-\dfrac{7}{8}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 10 2022
hệ số gốc là y=-3x+2 là -3
hệ số gốc của y=4x+17 là 4
2 tháng 12 2023
a:
Vẽ đường thẳng y=-3x-3
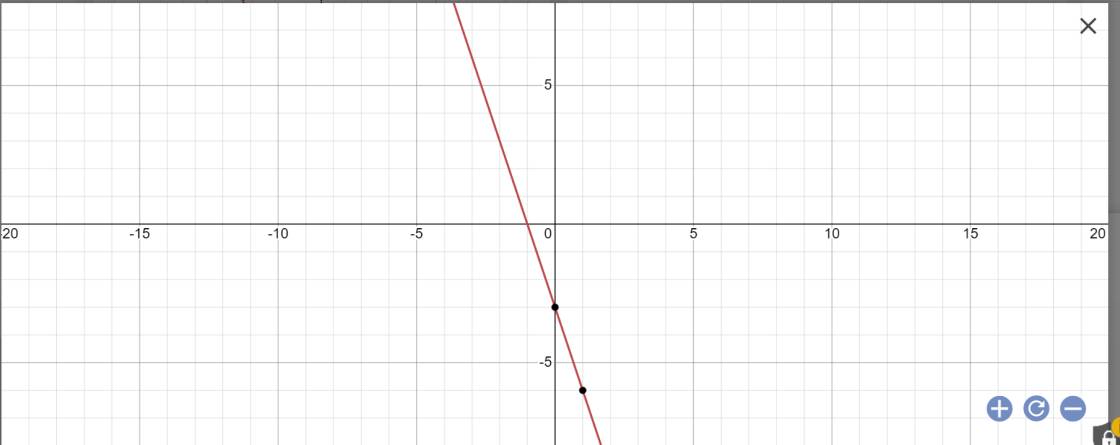
y=-3-3x
=>3x+y+3=0
Khoảng cách từ O đến đường thẳng y=-3x-3 là:
\(\dfrac{\left|0\cdot3+0\cdot1+3\right|}{\sqrt{3^2+1^2}}=\dfrac{3}{\sqrt{10}}\)
b:
Vẽ đường thẳng y=x
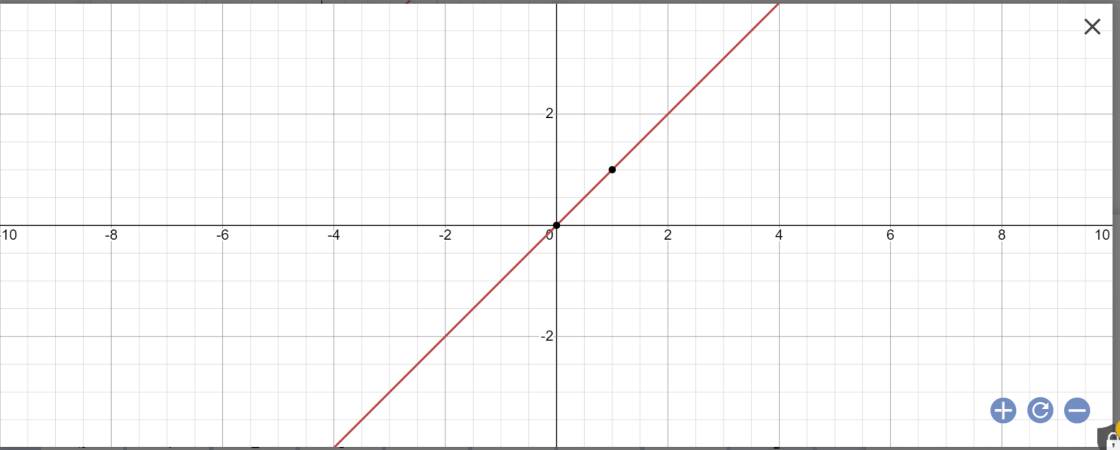
y=x
=>x-y=0
Khoảng cách từ O(0;0) đến đường thẳng y=x là:
\(\dfrac{\left|0\cdot1+0\cdot\left(-1\right)+0\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{0}{\sqrt{2}}=0\)
c:
Vẽ đồ thị y=-x
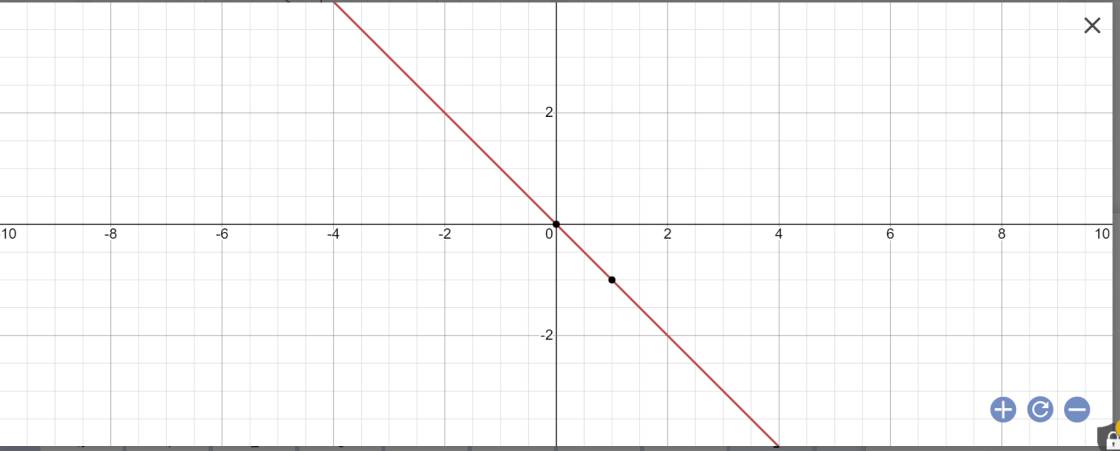
y=-x
=>x+y=0
Khoảng cách từ O(0;0) đến đường thẳng y=-x là:
\(\dfrac{\left|0\cdot1+0\cdot1+0\right|}{\sqrt{1^2+1^2}}=0\)
d:
Vẽ đồ thị hàm số y=1/2x
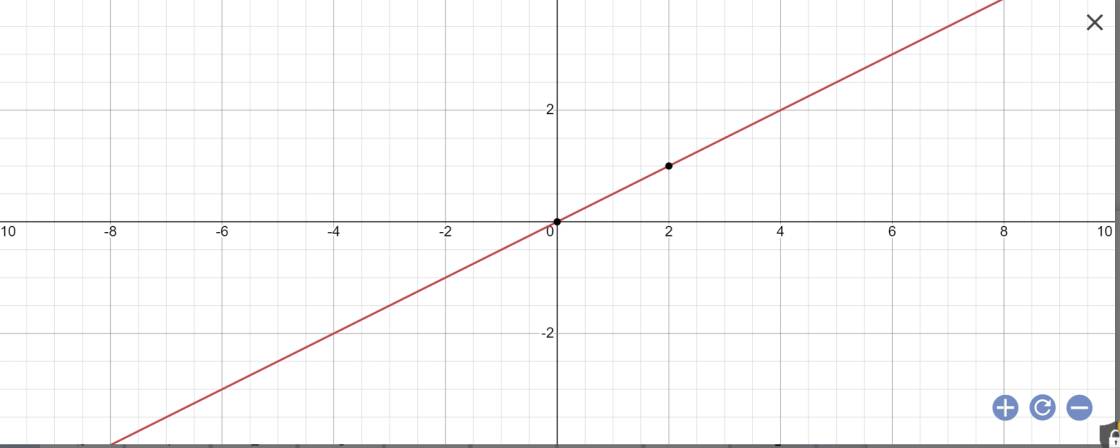
y=1/2x
=>1/2x-y=0
Khoảng cách từ O(0;0) đến đường thẳng y=1/2x là:
\(\dfrac{\left|0\cdot\dfrac{1}{2}+0\cdot\left(-1\right)+0\right|}{\sqrt{\left(\dfrac{1}{2}\right)^2+\left(-1\right)^2}}=\dfrac{0}{\sqrt{\dfrac{1}{4}+1}}=0\)
12 tháng 9 2023
a) Đường thẳng \(y=3x+6\) có hệ số góc \(a=3\Rightarrow\widehat{\left(Ox;d\right)=72^o\Rightarrow góc.nhọn}\)
b) Đường thẳng \(y=-4x+1\) có hệ số góc \(a=-4\Rightarrow\widehat{\left(Ox;d\right)=-76^o\Rightarrow góc.nhọn}\)
c) Đường thẳng \(y=-3x-6\) có hệ số góc \(a=-3\Rightarrow\widehat{\left(Ox;d\right)=-71^o\Rightarrow góc.nhọn}\)
HQ
Hà Quang Minh
Giáo viên
12 tháng 9 2023
a) Đường thẳng \(y = 3x + 6\) có hệ số góc là \(a = 3 > 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là góc nhọn.
b) Đường thẳng \(y = - 4x + 1\) có hệ số góc là \(a = - 4 < 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là tù.
c) Đường thẳng \(y = - 3x - 6\) có hệ số góc là \(a = - 3 < 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là tù.
HP
17 tháng 12 2020
Đường thẳng (d) có dạng \(y=kx+m\)
\(A\left(0;2\right)\in\left(d\right)\Rightarrow m=2\)
\(\Rightarrow y=kx+2\left(d\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm phân biệt khi phương trình \(x^2+\left(4-k\right)x+1=0\) có hai nghiệm phân biệt
\(\Leftrightarrow\Delta=\left(k-2\right)\left(k-6\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}k>6\\k< 2\end{matrix}\right.\)
Ta có \(x_1=\dfrac{k-4+\sqrt{k^2-8k+12}}{2}\Rightarrow y_1=\dfrac{k^2-4k+4+k\sqrt{k^2-8k+12}}{2}\)
\(\Rightarrow E\left(\dfrac{k-4+\sqrt{k^2-8k+12}}{2};\dfrac{k^2-4k+4+k\sqrt{k^2-8k+12}}{2}\right)\)
\(x_1=\dfrac{k-4-\sqrt{k^2-8k+12}}{2}\Rightarrow y_1=\dfrac{k^2-4k+4-k\sqrt{k^2-8k+12}}{2}\)
\(\Rightarrow F\left(\dfrac{k-4-\sqrt{k^2-8k+12}}{2};\dfrac{k^2-4k+4-k\sqrt{k^2-8k+12}}{2}\right)\)
Tọa độ trung điểm \(I\left(\dfrac{k-4}{2};\dfrac{k^2-4k+4}{2}\right)\)
\(x-2y+3=0\left(d'\right)\)
\(I\left(\dfrac{k-4}{2};\dfrac{k^2-4k+4}{2}\right)\in\left(d'\right)\Rightarrow\dfrac{k-4}{2}-\left(k^2-4k+4\right)+3=0\)
\(\Leftrightarrow2k^2-9k+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}k=\dfrac{9+\sqrt{33}}{2}\left(l\right)\\k=\dfrac{9-\sqrt{33}}{2}\left(tm\right)\end{matrix}\right.\)
\(\Leftrightarrow k=\dfrac{9-\sqrt{33}}{2}\)
P/s: Không biết đúng kh.
TK
16 tháng 5 2021
a) \(\sqrt{4x^2-4x+9}=3\)
Vì \(4x^2-4x+9=\left(2x-1\right)^2+8>0\)( Với mọi x )
Nên \(\sqrt{4x^2-4x+9}=3\)
⇔\(4x^2-4x+9=9\)
⇔\(4x^2-4x=0\)
⇔\(4x\left(x-1\right)=0\)
⇔\(\left[{}\begin{matrix}4x=0\\x-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)là nghiệm
Lời giải:
Hệ số góc của đường thẳng \(y=ax+b\) chính bằng $a$
Vậy:
Hsg của đường thẳng \(y=-3x+2\) là $-3$
Hsg của đường thẳng \(y=4x+17\) là $4$
Hsg của đường thẳng \(y=\frac{17}{18}x-\frac{7}{8}\) là \(\frac{17}{18}\)