2. Hình 4.17 có Ax / /By;OA⊥OB và A =145 . Tính số đo góc B.
3. Trong hình 4.18 có Ax / /By . Tính số đo của góc AOB.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác \(\Delta ABC\) và \(\Delta ADC\) có:
\(\begin{array}{l}AB = AD(gt)\\BC = DC(gt)\\AC\,\,\,chung\end{array}\)
Suy ra \(\Delta ABC = \Delta ADC\)(c.c.c)
Xét 2 tam giác ABC và tam giác ADC ta có :
AB = AD
BC = DC
AC chung
=> ΔABC = ΔADC

a) ta có: \(\widehat{BAx}+\widehat{ABy}=60^o+120^o=180^o\)
Mà 2 góc này là 2 góc trong cùng phía ⇒Ax//By
b) ta có: \(\widehat{CBy}+\widehat{BCz}=140^o+40^o=180^o\)
Mà 2 góc này là 2 góc trong cùng phía ⇒By//Cz
c) Ax//By, By//Cz⇒Ax//Cz
cảm ơn bạn nhiều lắm ko bt bạn sinh năm bao nhiêu để dễ xưng hô

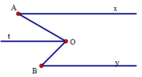 Qua điểm O kẻ tia Ot // Ox. Khi đó,
A
^
=
A
O
x
^
(2 góc so le trong).
Qua điểm O kẻ tia Ot // Ox. Khi đó,
A
^
=
A
O
x
^
(2 góc so le trong).
Do O t ∥ O x O y ∥ O x nên O t ∥ O y , B ^ = B O t ^ (2 góc so le trong)
Từ đó, ta có A O B ^ = A O t ^ + t O B ^ = A ^ + B ^ .
Vậy A ^ + B ^ = A O B ^ (đpcm)


Lời giải:
Ta thấy:
$\widehat{yBA}+\widehat{BAx}=124^0+56^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Ax$ (đpcm)

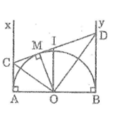
Chu vi hình thang ABDC bằng: AB + 2CD (chứng minh trên)
Suy ra: 14 = 4 + 2.CD ⇒ CD = 5 (cm)
Hay CM + DM = 5 ⇒ DM = 5 – CM (1)
Tam giác COD vuông tại O có OM ⊥ CD
Theo hệ thức lượng trong tam giác vuông, ta có:
O M 2 = CM.DM ⇔ 2 2 = CM.DM ⇔ 4 = CM.DM (2)
Thay (1) vào (2) ta có: CM.(5 – CM) = 4
⇔ 5CM – C M 2 – 4 = 0 ⇔ 4CM – C M 2 + CM – 4 = 0
⇔ CM(4 – CM) + (CM – 4) = 0 ⇔ CM(4 – CM) – (4 – CM) = 0
⇔ (CM – 1)(4 – CM) = 0 ⇔ CM – 1 = 0 hoặc 4 – CM = 0
⇔ CM = 1 hoặc CM = 4
Vì CM = CA (chứng minh trên) nên AC = 1 (cm) hoặc AC = 4 (cm)
Vậy điểm C cách điểm A 1cm hoặc 4cm thì hình thang ABDC có chu vi bằng 14.
2.Bên trong \(\widehat{AOB}\)kẻ tia \(Ot//Ax\).
\(\Rightarrow\widehat{OAx}+\widehat{AOt}=180^0\)(Trong cùng phía)
\(\Rightarrow\widehat{AOt}=180^0-\widehat{OAx}=180^0-145^0=35^0\)
Vì \(OA\perp OB\Rightarrow\widehat{AOB}=90^0\)
\(\Rightarrow\widehat{AOt}+\widehat{BOt}=90^0\)
\(\Rightarrow\widehat{BOt}=90^0-\widehat{AOt}=90^0-35^0=55^0\)
Vì \(\hept{\begin{cases}Ot//Ax\\By//Ax\end{cases}\Rightarrow Ot//By}\)
\(\Rightarrow\widehat{BOt}+\widehat{OBy}=180^0\)
\(\Rightarrow\widehat{OBy}=180^0-\widehat{BOt}=180^0-55^0=125^0\)
3.Kẻ tia Ot//Ax (tia Ot và tia By nằm trên cùng một nửa mặt phẳng bờ OA)
\(\Rightarrow\widehat{AOt}=\widehat{OAx}=50^0\)(so le trong)
Vì \(\hept{\begin{cases}Ot//Ax\\By//Ax\end{cases}\Rightarrow Ot//By}\)
\(\Rightarrow\widehat{BOt}+\widehat{OBy}=180^0\)(Trong cùng phía)
\(\Rightarrow\widehat{BOt}=180^0-\widehat{OBy}=180^0-150^0=30^0\)
\(\Rightarrow\widehat{AOB}=\widehat{AOt}-\widehat{BOt}=50^0-30^0=20^0\)