Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đây là cậu chép trg chỗ giải đáp rồi mà mk ko đc lm giống trg giải đáp

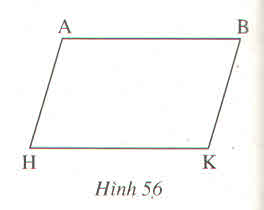
Nối A với K
Xét tam giác ABK và tam giác AHK có:
AK: cạnh chung
góc BAK = góc AKH (AB // HK)
góc HAK = góc AKB (AH //BK)
=> tam giác ABK = tam giác AHK
=> AB = HK (hai cạnh tương ứng)
Ta có: tam giác ABK = tam giác AHK
=> AH = BK (hai cạnh tương ứng)
kẻ đoạn thẳng AK
Xét tamgiác KAH và tam giác AKB
góc HAK = góc BKA (2 góc so le trong do AK cắt AH// BK )
cạnh AK chung
góc HKA = góc BAK (2 góc so le trong do AB //HK )
=> tam giác KAH = tam giác AKB ( g.c.g.)
=> AB=HK (2 cạnh tương ướng )
=> AH = BK (2 cạnh tương ướng )
đúng không..............................................

a/
\(Ax\perp m\left(gt\right);By\perp m\left(gt\right)\) => Ax//By (cùng vuông góc với m)
Mà Cz//Ax (gt)
=> Cz//By (cùng // với Ax)
b/
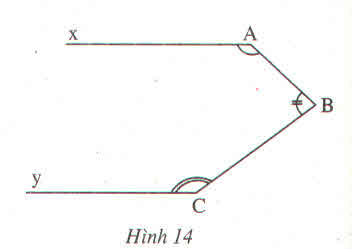
\(\widehat{BCz}=\widehat{ACB}-\widehat{C}=110^o-30^o=80^o\)
Ta có
Cz//By (cmt) \(\Rightarrow\widehat{BCz}=\widehat{CBy}=80^o\) (góc so le trong)
c/
\(CD\perp Ax\left(gt\right)\Rightarrow\widehat{ADC}=90^o\)
Cz//Ax (gt) \(\Rightarrow\widehat{A}=\widehat{C}=30^o\) (Góc so le trong)
Xét tg vuông ACD có
\(\widehat{ACD}=\widehat{ADC}-\widehat{A}=90^o-30^o=60^o\)

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) \(\Rightarrow\) \(\begin{cases} a = bk \\ c = dk \end{cases}\)
Ta có: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(1\right)\)
\(\dfrac{a.c}{b.d}=\dfrac{bk.dk}{b.d}=\dfrac{k^2.b.d}{b.d}=k^2\left(2\right)\)
Từ (1) và (2) suy ra: \(\dfrac{a.c}{b.d}=\dfrac{a^2+c^2}{b^2+d^2}\) \(\rightarrow đpcm\).

\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow ad=bc\)
Nếu:
\(\dfrac{a+b}{a}=\dfrac{c+d}{c}\Leftrightarrow c\left(a+b\right)=a\left(c+d\right)\)
\(ac+bc=ac+ad\)
\(bc=ad\)
\(\Leftrightarrow\dfrac{a+b}{a}=\dfrac{c+d}{c}\rightarrowđpcm\)
Đặt \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\)=k
=> a=k.b ; c=k.d
Ta có :
\(\dfrac{a+b}{a}\)=\(\dfrac{b.k+b}{b}\)=\(\dfrac{b.\left(k+1\right)}{b}\)=k+1 ( 1 )
\(\dfrac{c+d}{c}\)=\(\dfrac{d.k+d}{d}\)=\(\dfrac{d.\left(k+1\right)}{d}\)=k+1 ( 2 )
Từ (1) và (2) thì : \(\dfrac{a+b}{a}\)=\(\dfrac{c+d}{c}\)

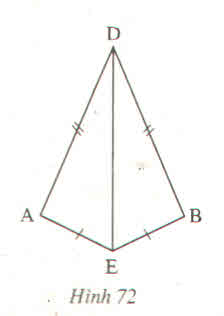
a) Xét \(\Delta ADE;\Delta BDE:\)
AD = BD (gt)
ED chung
AE = BE (gt)
\(\Rightarrow\Delta ADE=\Delta BDE\left(c.c.c\right)\)
b) Vì \(\Delta ADE=\Delta BDE\) (câu a)
nên \(\widehat{DAE}=\widehat{DBE}\) (2 góc t/ư).
Xem hình vẽ:
a) ∆ADE và ∆BDE có
DE cạnh chung
AD=DB(gt)
AE=BE(gt)
Vậy ∆ADE=∆BDE(c.c.c)
b) Từ ∆ADE=∆BDE(cmt)
Suy ra \(\widehat{DAE}\)=\(\widehat{DBE}\)(Hai góc tương ứng)

Đặt\(a+c=2b\left(1\right);2bd=c\left(b+d\right)\left(2\right)\\ \)
Thay (1) vào (2):\(\left(a+c\right)d=c\left(b+d\right)\)
Khai triển hết ra r rút gọn là ok.
Son Goku bạn giải hết ra giúp mik đi mik chậm hỉu lắm giúp mik đi mà!![]()
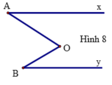




Do O t ∥ O x O y ∥ O x nên O t ∥ O y , B ^ = B O t ^ (2 góc so le trong)
Từ đó, ta có A O B ^ = A O t ^ + t O B ^ = A ^ + B ^ .
Vậy A ^ + B ^ = A O B ^ (đpcm)