Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đây là cậu chép trg chỗ giải đáp rồi mà mk ko đc lm giống trg giải đáp

a) △ABC có : Hai đường cao BE và AD mà 2 đường này cùng cắt nhau tại điểm I ⇒ I là trực tâm
⇒ CI là đường cao còn lại ⇒ CI ⊥ AB
b) Xét △BEC có : góc EBC + gócBEC + góc BCE = \(180^0\)( định lí tổng ba góc )
⇒ góc EBC = \(180^0\) - góc BEC - góc BCE = \(180^0\)- \(90^0\)-\(40^0\)= \(50^0\)
Lại xét △BID có : góc BID + góc IBD + góc BDI = \(180^0\)
⇒ góc BID = \(180^0\) - \(90^0\) - \(50^0\) = \(40^0\)
Có góc BID + góc DIE = \(180^0\)( 2 góc kề bù )
⇒ góc DIE = \(180^0\) - góc BID = \(180^0-40^0\)= \(140^0\)

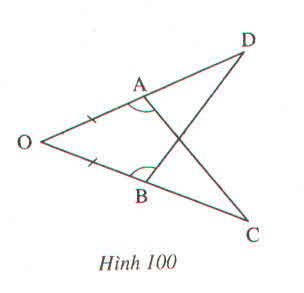
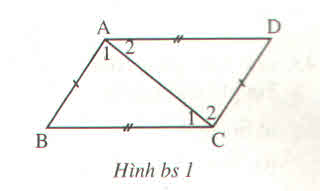
\(\widehat{A}_1=\widehat{C}_2;\widehat{A}_2=\widehat{C}_1;\widehat{B}=\widehat{D}\)

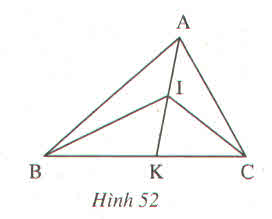
a)Ta có \(\widehat{BIK}\) là góc ngoài của BAI.
Nên \(\widehat{BIK}>\widehat{BAI}\) (1)
b) \(\widehat{CIK}>\widehat{CAI}\)( Góc ngoài của \(\Delta\) CAI)
Từ (1) và (2) ta có:
\(\widehat{BIK}+\widehat{CIK}>\widehat{BAI}+\widehat{CAI}\)
\(\Rightarrow\widehat{BIC}>\widehat{BAC}\)
) Ta có ∠BIK là góc ngoài của ∠BAI( hay là góc ngoài ∠BAK)
Các em lưu ý nếu không hiểu: Góc ngoài của tam giác lớn hơn mỗi ngóc trong không kề với nó (ở đây là tam giác ∆ BIA)
Nên ∠BIK > ∠BAK (1)
b) Góc ∠CIK > ∠CAI (2) (Góc ngoài của ∆ CAI)
Từ (1) và (2) ta có: ∠BIK + ∠CIK > ∠BAK + ∠CAI
Mà ∠BIC = ∠BIK + ∠CIK; ∠BAC = ∠BAK + ∠CAI
⇒ ∠BIC > ∠BAC.

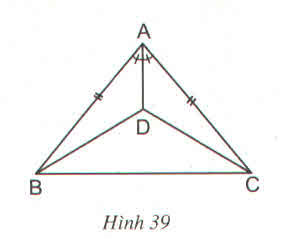
a) Căn cứ các kí hiệu đã cho trên hình của bài 39 ta có: ∆ABD và ∆ACD có:
AB = AC
ˆBAD=ˆCADBAD^=CAD^
AD là cạnh chung
=> ∆ABD = ∆ACD
b) Vì ∆ABD = ∆ACD
=> BD = CD => ∆BCD cân tại D
=> ˆDBC=ˆDCB
Hướng dẫn:
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210

c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL

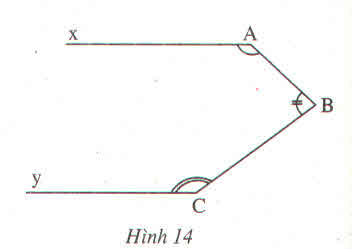
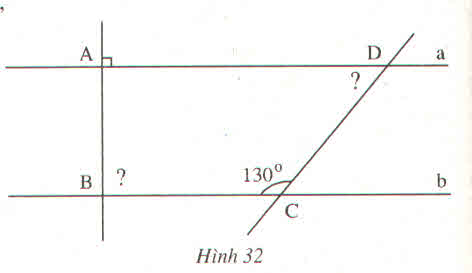
Ta có a // b, nên
góc B = góc A = 90 độ (đồng vị)
Ta lại có \(\widehat{C}+\widehat{D}=180^o\)
hay \(130^o+\widehat{D}=180^o\Rightarrow\widehat{D}=180^o-130^o=50^o\)
vậy góc B = 90 độ
góc C = 50 độ
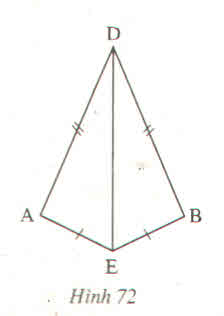




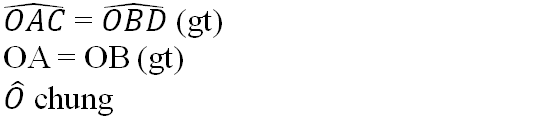


a) Xét \(\Delta ADE;\Delta BDE:\)
AD = BD (gt)
ED chung
AE = BE (gt)
\(\Rightarrow\Delta ADE=\Delta BDE\left(c.c.c\right)\)
b) Vì \(\Delta ADE=\Delta BDE\) (câu a)
nên \(\widehat{DAE}=\widehat{DBE}\) (2 góc t/ư).
Xem hình vẽ:
a) ∆ADE và ∆BDE có
DE cạnh chung
AD=DB(gt)
AE=BE(gt)
Vậy ∆ADE=∆BDE(c.c.c)
b) Từ ∆ADE=∆BDE(cmt)
Suy ra \(\widehat{DAE}\)=\(\widehat{DBE}\)(Hai góc tương ứng)