Ba hình vuông ABCD; BNMC; NPQM bằng nhau, xếp kề nhau. AQ cắt BC và cắt NM tại I và K. Biết AB = 4cm.
a/ Tính diện tích tam giác AID
b/ Tính diện tích tam giác DIK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

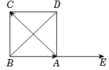
Vẽ A E → = B A → .
Khi đó cos A C → , B A → = cos A C → , A E →
= cos C A E ^ = cos 135 0 = − 2 2 .
Chọn B.

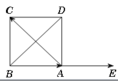
Vẽ A E → = B A → .
Khi đó cos A C → , B A → = cos A C → , A E →
= cos C A E ^ = cos 135 0 = − 2 2 .
Chọn B.

: Ký hiệu (a) là số đo góc a, đặt (CDK)=x
trên tia đối tia AB lấy điểm F sao cho AF = KC
như vậy tam giác ADF bằng tam giác CDK nên góc (ADF)=(CDK)=(KDE)=x
góc (FED)=(EDC)=2x (so le trong)
(FDE)=x+(90-2x)= 90-x
(EFD) = 180 - (FED) - (FDE) = 180 -( 2x) -(90-x) = 90-x = (FDE) vậy tam giác FED cân tại E hay DE =FE = FA +AE =KC + AE dpcm

a) Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\); \(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \)
Mà \(AE = BF = CG = HD\) (gt) suy ra \(BE = CF = DG = AH\)
Xét \(\Delta AEH\) và \(\Delta DHG\) ta có:
\(\widehat {\rm{A}} = \widehat {\rm{D}} = 90\)
\(AE = GH\) (gt)
\(AH = DG\) (gt)
Suy ra \(\Delta AEH = \Delta DHG\) (c-g-c)
Suy ra \(\widehat {{\rm{AEH}}} = \widehat {{\rm{DHG}}}\) (hai góc tương ứng)
Mà \(\widehat {AEH} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {DHG} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {EHG} = 90^\circ \)
Chứng minh tương tự ta được \(\widehat {HGF} = 90^\circ ;\;\widehat {GFE} = 90^\circ \)
Vậy tứ giác \(EFGH\) là một góc vuông
b) Vì \(\Delta AEH = \Delta DHG\) (cmt)
Suy ra \(HE = HG\) (2)
Từ (1) và (2) suy ra \(EFGH\) là hình vuông
c) chứng minh tương tự câu b ta có: \(HE = EF\); \(HE = FG\)
Khi đó \(EFGH\) có \(HE = HG = EF = FG\) nên là hình thoi (3)
Tứ giác \(EFGH\) có ba góc vuông nên là hình chữ nhật (4)
Từ (3) và (4) suy ra \(EFGH\) là hình vuông
A B C D M N P Q I K
DQ=DC+CM+MQ=4+4+4=12 cm
AD=AB=4 cm
\(S_{ADQ}=\dfrac{ADxDQ}{2}=\dfrac{4x12}{2}=24cm^2\)
Hai tg ABI và tg KBI có chung BI, đường cao từ A->BC = đường cao từ K->BC nên
\(S_{ABI}=S_{KBI}\Rightarrow\dfrac{S_{ABI}}{S_{KBI}}=1\)
Hai tg trên có chung đường cao từ B->AQ nên
\(\dfrac{S_{ABI}}{S_{KBI}}=\dfrac{AI}{IK}=1\Rightarrow AI=IK\)
Hai tg INK và tg QNK có chung NK và đường cao từ I->MN = đường cao từ Q->MN nên \(S_{INK}=S_{QNK}\Rightarrow\dfrac{S_{INK}}{S_{QNK}}=1\)
Hai tg trên có chung đường cao từ N->AQ nên
\(\dfrac{S_{INK}}{S_{QNK}}=\dfrac{IK}{KQ}=1\Rightarrow IK=KQ\)
\(\Rightarrow AI=IK=KQ=\dfrac{AQ}{3}\)
a/ Hai tg AID và tg ADQ có chung đường cao từ D->AQ nên
\(\dfrac{S_{AID}}{S_{ADQ}}=\dfrac{AI}{AQ}=\dfrac{1}{3}\Rightarrow S_{AID}=\dfrac{S_{ADQ}}{3}=\dfrac{24}{3}=8cm^2\)
Hai tg DIK và tg ADQ có chung đường cao từ D->AQ nên
\(\dfrac{S_{DIK}}{S_{ADQ}}=\dfrac{IK}{AQ}=\dfrac{1}{3}\Rightarrow S_{DIK}=\dfrac{S_{ADQ}}{3}=\dfrac{24}{3}=8cm^2\)