Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

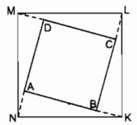
Xét △ ANK và △ BKL :
AN = BK (gt)
∠ A = ∠ B = 90 0
AK = BL (vì AB = BC, BK = CL)
Do đó △ ANK = △ BKL (c.g.c)
⇒ NK = KL (1)
Xét △ BKL và △ CLM:
BK = CL (gt)
∠ B = ∠ C = 90 0
BL = CM (vì BC = CD, CL = DM)
Do đó: △ BKL = △ CLM (c.g.c)
⇒ KL = LM (2)
Xét △ CLM và △ DMN :
CL = DM (gt)
∠ C = ∠ D = 90 0
CM = DN (vì CD = DA, DM = AN)
Do đó: △ CLM = △ DMN (c.g.c)
⇒ LM = MN (3)
Từ (1), (2) và (3) ⇒ NK = KL = LM = MN
Tứ giác MNKL là hình thoi
△ ANK = △ BKL ⇒ ∠ (ANK) = ∠ (BKL)
Trong tam giác ANK có A là góc vuông ⇒ ∠ (ANK) + ∠ (AKN) = 90 0
⇒ ∠ (BKL) + ∠ (AKN) = 90 0 hay ∠ (NKL) = 90 0
Vậy tứ giác MNKL là hình vuông.

a: Sửa đề: ΔAEF vuông cân tại A
Xét ΔADF vuông tại D và ΔABE vuông tại B có
AD=AB
DF=BE
Do đó: ΔADF=ΔABE
=>AF=AE và \(\widehat{DAF}=\widehat{BAE}\)
mà \(\widehat{BAE}+\widehat{DAE}=90^0\)
nên \(\widehat{DAF}+\widehat{DAE}=90^0\)
=>\(\widehat{FAE}=90^0\)
Xét ΔAEF có \(\widehat{FAE}=90^0\) và AE=AF
nên ΔAEF vuông cân tại A
b: Gọi giao điểm của AH với EF là M
H đối xứng A qua EF
=>EF là đường trung trực của HA
=>EH=EA và FH=FA
mà AH=AE
nên EH=EA=FH=FA
Xét tứ giác AEHF có
AE=HE=HF=FA
nên AEHF là hình thoi
Hình thoi AEHF có \(\widehat{FAE}=90^0\)
nên AEHF là hình vuông

: Ký hiệu (a) là số đo góc a, đặt (CDK)=x
trên tia đối tia AB lấy điểm F sao cho AF = KC
như vậy tam giác ADF bằng tam giác CDK nên góc (ADF)=(CDK)=(KDE)=x
góc (FED)=(EDC)=2x (so le trong)
(FDE)=x+(90-2x)= 90-x
(EFD) = 180 - (FED) - (FDE) = 180 -( 2x) -(90-x) = 90-x = (FDE) vậy tam giác FED cân tại E hay DE =FE = FA +AE =KC + AE dpcm