Cho hình chữ nhật ABCD, từ A hạ vuông góc với AC, cắt AC ở H. Biết rằng AB=13cm; DH=5cm. Khi đó BH=..cm (Nhập kết quả dưới dạng phân số tối giản)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
HN
27 tháng 6 2018
Theo đinh lý Pytago trong tam giác HCD có:
\(HC^2+HD^2=CD^2\)
\(\Rightarrow HC=\sqrt{13^2-5^2}=12\)
Lại có: \(CD^2=HC.AC\)
\(\Rightarrow13^2=12.AC\)
\(\Rightarrow AC=\frac{169}{12}\approx14,1\)
\(\Rightarrow BD\approx14,1\)(cm)
18 tháng 10 2015
ta có tam giác DHC đồng dạng với tam giác ADC
==> DC.AD = AC.DH
==> sqr(DC.AD) = SQR(AC.DH)
mà AD^2 = AC^2 - DC^2
==> 169( AC^2 - 169) = 25.AC^2
=> AC= 169/12
NA
15 tháng 7 2018
Xét tam giác DHC vuông tại H
\(\Rightarrow HC=\sqrt{DC^2-DH^2}=12\left(cm\right)\)
Xét tam giác ADC vuông tại D đường cao DH
\(\Rightarrow AH=\dfrac{DH^2}{HC}=\dfrac{25}{12}\)
\(\Rightarrow AC=AH+HC=\dfrac{169}{12}\)(cm)
\(\Rightarrow BD=\dfrac{169}{12}\)(cm)
HT
0
14 tháng 10 2021
a: Ta có: AD//BC
AC\(\perp\)AD
Do đó: AC\(\perp\)BC
Xét ΔBAK vuông tại A có AC là đường cao ứng với cạnh huyền BK, ta được:
\(CB\cdot CK=AC^2\left(1\right)\)
Xét ΔADC vuông tại A có AH là đường cao ứng với cạnh huyền CD,ta được:
\(CH\cdot CD=AC^2\left(2\right)\)
Từ (1) và(2) suy ra \(CB\cdot CK=CH\cdot CD\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 7 2021
Pitago tam giác vuông ACD:
\(AC=\sqrt{AD^2+CD^2}=\sqrt{AD^2+AB^2}=20\)
Hệ thức lượng tam giác vuông ABC với đường cao BH:
\(AB^2=AH.AC\Rightarrow AH=\dfrac{AB^2}{AC}=\dfrac{64}{5}\)
\(HC=AC-AH=\dfrac{36}{5}\)
b.
Hai tam giác vuông ADC và AHF có chung góc \(\widehat{HAD}\)
\(\Rightarrow\Delta_VADC\sim\Delta_VAHF\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AH}=\dfrac{AC}{AF}\Rightarrow AD.AF=AC.AH\) (1)
Mặt khác theo hệ thức lượng tam giác vuông ABC:
\(AB^2=AH.AC\) (2)
(1);(2) \(\Rightarrow AD.AF=AB^2\)
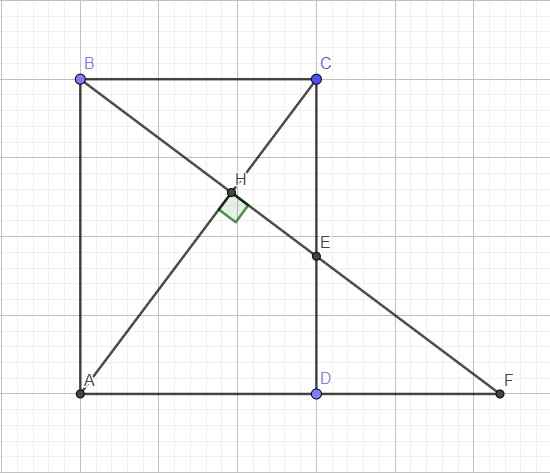
Do ABCD là hình chữ nhật => CD = AB = 13 cm và BD = AC
Áp dụng định lí Pi-ta-go vào tam giác vuông DHC có:
HC^2 = CD^2 - DH^2 = 13^2 - 5^2 = 12^2 => HC = 12 cm
Áp dụng hệ thức lượng vào tam giác vuông ACD có:
CD^2 = HC.AC => AC = CD^2/HC = 13^2/12 = 169/12 cm
Vậy BD = AC = 169/12 cm.