Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có ∠C = 180o - 60o - 30o = 90o
Vì ∠C > ∠A > ∠B ⇒ AB > BC > AC. Chọn C
\(\widehat{ACB}=180^0-60^0-40^0=80^0\)
=>\(\widehat{KCB}=\dfrac{80^0}{2}=40^0\)
mà \(\widehat{KBC}=40^0\)
nên \(\widehat{KCB}=\widehat{KBC}\)
=>ΔKBC cân tại K
hay KB=KC
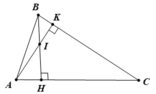
b. Trong tam giác vuông ABH có ∠(ABH) + ∠(AHB) + ∠(BAH) = 180o
Nên ∠(ABH) = 180o - 60o - 90o = 30o ( 1 điểm)
Trong tam giác vuông ABK có (BAK) + (ABK) + (BKA) = 180o
Nên ∠(BAH) = 180o - 70o - 90o = 20o ( 1 điểm)
Trong tam giác ABM có ∠(ABI) + ∠(BAI) + ∠(IAB) = 180onên
∠(AMB) = 180o - 20o - 30o = 130o ( 1 điểm)
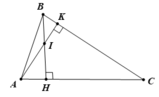
b. Trong tam giác vuông ABH có ∠(ABH) + ∠(AHB) + ∠(BAH) = 180o
Nên ∠(ABH) = 180o - 60o - 90o = 30o ( 1 điểm)
Trong tam giác vuông ABK có (BAK) + (ABK) + (BKA) = 180o
Nên ∠(BAH) = 180o - 70o - 90o = 20o ( 1 điểm)
Trong tam giác ABM có ∠(ABI) + ∠(BAI) + ∠(IAB) = 180onên
∠(AMB) = 180o - 20o - 30o = 130o ( 1 điểm)
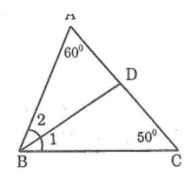
Trong ΔABC ta có:
∠A + ∠B + ∠C = 180o(tổng ba góc trong tam giác)
⇒∠B = 180o - (∠A +∠C )
⇒x = 180o - (60o + 50o) = 70o
(∠B1) =(∠B2 ) = (1/2 )∠B (vì BD là tia phân giác)
⇒ ∠B1 = ∠B2 = 70o : 2 = 35o
Trong ΔBCD ta có ∠(ADB) là góc ngoài tại đỉnh D
⇒ ∠(ADB) = ∠(B1 ) + ∠C (tính chất góc ngoài tam giác)
Nên ∠(ADB) = 35º + 50º = 85º
+) Do ∠(ADB) + ∠(BDC) = 180o(hai góc kề bù)
⇒∠(BDC) = 180o-∠(ADB) = 180o - 85o = 95o
a) Vì BD=BA = 2cm suy ra tam giác BAD cân tại D, mà góc BAD = 600
suy ra tam giác BAD đều
b) Xét tam giác ABH và tam giác ADH
có AB=AD ( tam giác BAD đều)
AH chung
HB=HD (GT)
suy ra tam giác ABH = tam giác ADH (c.c.c) (*)
suy ra góc AHB=góc AHD (góc tương ứng) (1)
mà góc AHB kề bù góc AHD (2)
Từ (1) và (2) suy ra góc AHB=góc AHD = 900
suy ra AH vuông góc với BD tại H
Từ (*) suy ra BH=HD =BD:2=1 cm
mà BC=BH+HC suy ra 5=1+HC suy ra HC=4cm
Xét tam giác ABH vuông tại H
có AB2=BH2+AH2 (Đ/l pytago)
suy ra 4=1+AH2 suy ra AH=\(\sqrt{3}\)\(\sqrt{19}\) vì AH >0
Xét tam giác AHC vuông tại H
có AH2+HC2=AC2 suy ra 3 + 16 = AC2 suy ra AC=\(\sqrt{19}\) (cm)
ta có AB2=22=4 cm; BC2=25 cm, AC2=19 cm
suy ra AB <AC<BC
tam giác ABC có AB <AC<BC nên góc C < góc B<góc A
góc A >600
Từ đó lập luận so sánh tiếp nhé
Chúc các em học tốt!!!
Hình vẽ nhé